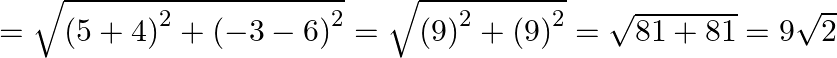Login/Sign Up
Home » If Q (0, 1) is equidistant from P (5, – 3) and R (x, 6), find the values of x. Also find the distance QR and PR.
If Q (0, 1) is equidistant from P (5, – 3) and R (x, 6), find the values of x. Also find the distance QR and PR.
CBSE | Class 10 | Coordinate Geometry | Maths | NCERT
If Q (0, 1) is equidistant from P (5, – 3) and R (x, 6), find the values of x. Also find the distance QR and PR.

Solution:

Given: PQ = QR because Q (0, 1) is equidistant between P (5, – 3) and R (x, 6).

Step 1: Using the distance formula, calculate the distance between PQ and QR.

PQ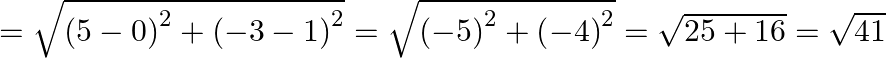=\sqr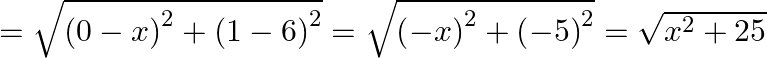t{{{\left( 5-0 \right)}^{2}}+{{\left( -3-1 \right)}^{2}}}=\sqrt{{{\left( -5 \right)}^{2}}+{{\left( -4 \right)}^{2}}}=\sqrt{25+16}=\sqrt{41}

QR=\sqrt{{{\left( 0-x \right)}^{2}}+{{\left( 1-6 \right)}^{2}}}=\sqrt{{{\left( -x \right)}^{2}}+{{\left( -5 \right)}^{2}}}=\sqrt{{{x}^{2}}+25}

Step 2: Use PQ=QR

To omit the square root, square both sides.

    \[41\text{ }=\text{ }{{x}^{2~}}+\text{ }25\]

    \[{{x}^{2~}}=\text{ }16\]

    \[x\text{ }=\text{ }\pm \text{ }4\]

    \[x\text{ }=\text{ }4\text{ }or\text{ }x\text{ }=\text{ }-4\]

R (4, 6) or R (-4, 6) will be the coordinates of Point R.

If R (4, 6), then

QR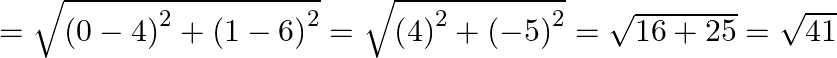=\sqrt{{{\left( 0-4 \right)}^{2}}+{{\left( 1-6 \right)}^{2}}}=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( -5 \right)}^{2}}}=\sqrt{16+25}=\sqrt{41}

PR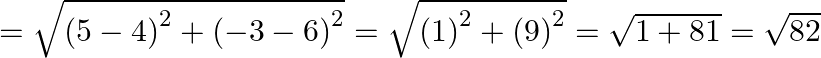=\sqrt{{{\left( 5-4 \right)}^{2}}+{{\left( -3-6 \right)}^{2}}}=\sqrt{{{\left( 1 \right)}^{2}}+{{\left( 9 \right)}^{2}}}=\sqrt{1+81}=\sqrt{82}

If R (-4, 6), then,

QR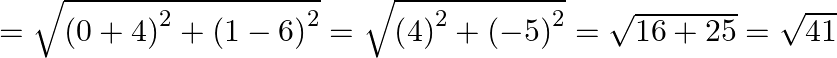=\sqrt{{{\left( 0+4 \right)}^{2}}+{{\left( 1-6 \right)}^{2}}}=\sqrt{{{\left( 4 \right)}^{2}}+{{\left( -5 \right)}^{2}}}=\sqrt{16+25}=\sqrt{41}

PR=\sqrt{{{\left( 5+4 \right)}^{2}}+{{\left( -3-6 \right)}^{2}}}=\sqrt{{{\left( 9 \right)}^{2}}+{{\left( 9 \right)}^{2}}}=\sqrt{81+81}=9\sqrt{2}

i

More Material