Solution:
![]() (as given)
(as given)
![]() is invertible if
is invertible if ![]() is a bijection (i.e one-one onto function)
is a bijection (i.e one-one onto function)
One-One function
Suppose ![]() be two arbitrary elements in
be two arbitrary elements in ![]()
Therefore, ![]()
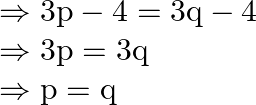
When ![]()
Therefore, ![]() is one-one function.
is one-one function.
Onto function
Suppose ![]() be an arbitrary element of
be an arbitrary element of ![]() (Co-domain)
(Co-domain)
Then, ![]()
![]()
![]()
![]() Since
Since ![]()
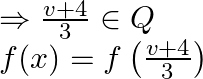
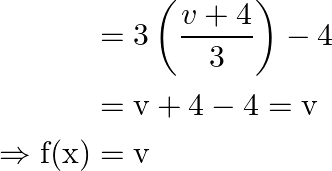
Therefore this shows that every element in the co-domain has its pre-image in domain.
Hence, ![]() is onto function.
is onto function.
As a result, ![]() is invertible.
is invertible.
Now we need to find ![]() ,
,
Suppose ![]()
![]()
Now, replace all ![]() with y and all y with
with y and all y with ![]() .
.
Now, solve for y
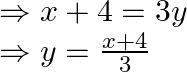
Now replace ![]() with
with ![]()
As a result, ![]()
