Solution:
![]() and
and ![]() is even
is even ![]() (As given)
(As given)
If ![]() is Reflexive, Symmetric and Transitive, then
is Reflexive, Symmetric and Transitive, then ![]() is an equivalence relation.
is an equivalence relation.
Reflexivity:
Suppose a be an arbitrary element of ![]()
![]()
As ![]() is even
is even
![]()
Therefore, ![]() is reflexive.
is reflexive.
Symmetric:
Suppose a and ![]() , such that
, such that ![]()
![]() even.
even.
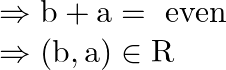
Therefore, ![]() is symmetric.
is symmetric.
Transitivity:
Suppose ![]() and
and ![]() , such that
, such that ![]() and
and ![]()
![]() (which is an even)
(which is an even)
and ![]() (which is an even)
(which is an even)
On adding both the above equations, we obtain
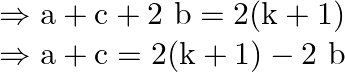
![]() is an even number
is an even number
![]()
Therefore, ![]() is transitive.
is transitive.
As a result, ![]() is an equivalence relation.
is an equivalence relation.
