(i) x – √3y + 8 = 0
Given:
The condition is
![]()
Condition of line in typical structure is given by
![]()
where ‘θ’ is the point among opposite and positive x pivot and ‘p’ is opposite separation from beginning.
So presently,
![]()
![]()
Separation both the sides by
![]()
![]()
![]()
This is as:
![]()
∴ The above condition is of the structure, where
![]()
and
![]()
Opposite distance of line from beginning
![]()
Point among opposite and positive x –axis
![]()
![]()
Given:
The condition is
![]()
Condition of line in typical structure is given by
![]()
where ‘θ’ is the point among opposite and positive x pivot and ‘p’ is opposite separation from beginning.
So presently,
![]()
Separation the two sides by
![]()
![]()
This is as:
![]()
∴ The above condition is of the structure
![]()
, where
![]()
and
![]()
Opposite distance of line from beginning
![]()
Point among opposite and positive x –axis
![]()

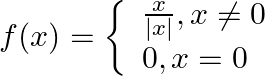 . Show that
. Show that 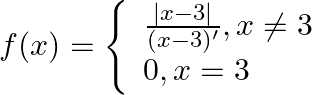 . Show that
. Show that