Solution:
![]() and
and ![]() is even
is even ![]() where
where ![]()
(As given)
If ![]() is Reflexive, Symmetric and Transitive, therefore
is Reflexive, Symmetric and Transitive, therefore ![]() equivalence relation.
equivalence relation.
Reflexivity:
Suppose ![]() be an arbitrary element of A
be an arbitrary element of A
![]()
As 0 is even
![]()
Therefore, ![]() is reflexive.
is reflexive.
Symmetric:
Suppose ![]() and
and ![]() , such that
, such that ![]()
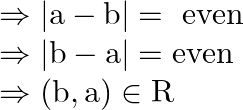
Therefore, ![]() is symmetric.
is symmetric.
Transitivity:
Suppose ![]() and
and ![]() , such that
, such that ![]() and
and ![]()
![]() is even and
is even and ![]() is even
is even
This is only possible when ![]() and
and ![]() both are even or odd and
both are even or odd and ![]() and
and ![]() both are even or odd.
both are even or odd.
Two cases arise:
Case I: If ![]() is an even
is an even
Suppose ![]() and
and ![]()
![]() is even and
is even and ![]() is even
is even
As ![]() is even
is even
![]() a is even and
a is even and ![]() is even
is even
![]() is even
is even
![]()
Case II: If b is an odd
Suppose ![]() and
and ![]()
![]() is even and
is even and ![]() is even
is even
![]() As
As ![]() is odd
is odd
![]() is odd and
is odd and ![]() is odd
is odd
As difference of two odd numbers is even
![]() is even
is even
![]()
Therefore, R is transitive.
As a result, R is an equivalence relation.
