Solution:
The given inequalities are
![]()
For
![]()
Let us put the value of
![]()
and
![]()
in equation one by one, we get
![]()
and
![]()
Therefore, we got points as
![]()
and
![]()
Now check for the origin
![]()
We got
![]()
,which is not true.
We can say that the origin would not lie in the solution area. The required region would be on the right of line`s graph.
Now for
![]()
Let us put the value of
![]()
and
![]()
in equation one by one, we get
![]()
and
![]()
Let us take
![]()
we get
![]()
Therefore, the points for the given inequality are
![]()
and
![]()
As we can see that the origin lies on the given equation
Now we will check for
![]()
point to check which side of the line`s graph will be included in the solution.
We get
![]()
which is not true
Therefore, the required region would be on the left side of the line
![]()
In the below graph the shaded region is the required solution of the inequalities.


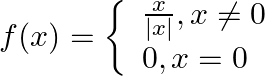 . Show that
. Show that 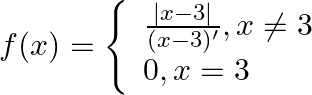 . Show that
. Show that