Solution:
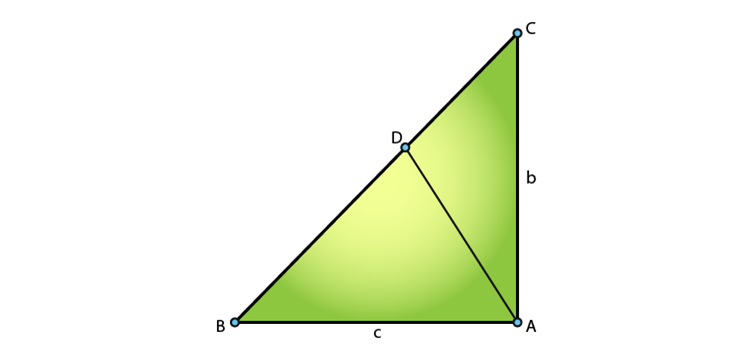
We have,
In ∆BAC, by Pythagoras theorem, we have
![\[\begin{array}{*{35}{l}} <!-- /wp:paragraph --> <!-- wp:paragraph --> B{{C}^{2}}~=\text{ }A{{B}^{2}}~+\text{ }A{{C}^{2}} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \Rightarrow B{{C}^{2}}~=\text{ }{{c}^{2}}~+\text{ }{{b}^{2}} \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \Rightarrow BC~=\text{ }\surd ({{c}^{2}}~+\text{ }{{b}^{2}}) \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-949dbdc15a70bb8a7d24dc30a1b92659_l3.png "Rendered by QuickLaTeX.com")
![\[\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-1833cc7760eba792ec467db2c623cfe8_l3.png "Rendered by QuickLaTeX.com")
In ∆ABD and ∆CBA
∠B = ∠B [Common]
∠ADB = ∠BAC
![\[\left[ Each\text{ }90{}^\circ \right]\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-97caa69fe78fe3af9376eb3114ec6cd5_l3.png "Rendered by QuickLaTeX.com")
Then, ∆ABD ͏~ ∆CBA [By AA similarity]
Thus,
AB/ CB = AD/ CA [Corresponding parts of similar triangles are proportional]
![\[\begin{array}{*{35}{l}} <!-- /wp:paragraph --> <!-- wp:paragraph --> c/\text{ }\surd ({{c}^{2}}~+\text{ }{{b}^{2}})\text{ }=\text{ }AD/\text{ }b \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \therefore AD\text{ }=\text{ }bc/\text{ }\surd ({{c}^{2}}~+\text{ }{{b}^{2}}) \\ <!-- /wp:paragraph --> <!-- wp:paragraph --> \end{array}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-490e8d1354e974cd708e106d108e7163_l3.png "Rendered by QuickLaTeX.com")
![\[.\text{ }\mathbf{4}.\mathbf{219}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-e0e6c8ae5a8e273c9a6be45b04989009_l3.png "Rendered by QuickLaTeX.com")
Solution:
We have,
In ∆BAC, by Pythagoras theorem, we have
In ∆ABD and ∆CBA
∠B = ∠B [Common]
∠ADB = ∠BAC
Then, ∆ABD ͏~ ∆CBA [By AA similarity]
Thus,
AB/ CB = AD/ CA [Corresponding parts of similar triangles are proportional]