Solution: Let's say that $n$ be any arbitrary positive odd integer. Upon dividing $n$ by 6, let $m$ be the quotient and $r$ be the remainder. Therefore, by Euclid's division lemma, we get $n=6 m+r$,...
Using Euclid’s algorithm, find the HCF of
(i) 405 and 2520
(ii) 504 and 1188
Solution: (i) When applying Euclid's algorithm, that is dividing $2520$ by $405$, we obtain, Quotient $=6$, Remainder $=90$ $\therefore 2520=405 \times 6+90$ Again upon applying Euclid's algorithm,...
What do you mean by Euclid’s division algorithm?
Solution: It is stated by the Euclid's division algorithm that for any two positive integers $a$ and $b$, there exist unique integers $q$ and $r$, such that $a=b q+r$. where $0 \leq r \leq b$.
The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, p q what can you say about the prime factors of q? (i) 43.123456789 (ii) 0.120120012000120000. . .(iii) ![Rendered by QuickLaTeX.com \[43.\overline{123456789}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-817e128760c54fb2ce3df345c7c4a60a_l3.png)
(i) 43.123456789 Since it has a terminating decimal expansion, it is a rational number in the form of p/q and q has factors of 2 and 5 only. (ii) 0.120120012000120000. . . Since, it has...
Prove that one and only one out of n, n + 2 and n + 4 is divisible by 3, where n is any positive integer.
Solution: According to Euclid’s division Lemma, Let n be the positive integer And b equals to 3 Where q is the quotient and r is the remainder $n\text{ }=3q+r$, 0<r<3 implies remainders may be...
Show that the cube of a positive integer of the form 6q + r, q is an integer and r = 0, 1, 2, 3, 4, 5 is also of the form 6m + r.
Solution: Where q is an integer and r = 0, 1, 2, 3, 4, 5, then 6q + r is a positive integer. The positive integers are then of the form: 6q, 6q+1, 6q+2, 6q+3, 6q+4, and 6q+5. Taking cube on L.H.S...
Prove that if x and y are both odd positive integers, then x2 + y2 is even but not divisible by 4.
Solution: Let x and y be 2k + 1 and 2p + 1 the two odd positive numbers, respectively Therefore, ${{x}^{2}}~+\text{ }{{y}^{2}}~=\text{ }{{\left( 2k+\text{ }1 \right)}^{2}}~+{{\left( 2p\text{ }+1...
If n is an odd integer, then show that n2 – 1 is divisible by 8.
Solution: Any odd positive integer n can be written in the form 4q + 1 or 4q + 3 as we know. Now, according to the question, For $n~=4q~+1$, Therefore ${{n}^{2}}~-1\text{ }={{\left( 4q~+\text{ }1...
Show that the square of any odd integer is of the form 4q + 1, for some integer q.
Solution: Let b=4 and a be any odd integer. According to Euclid’s algorithm, For some integer $m\ge ~0,\text{ }a=4m+r$ And r = 0,1,2,3 as 0 ≤ r < 4. As a result we have, a = 4m or 4m +...
Show that the square of any positive integer cannot be of the form 6m + 2 or 6m + 5 for any integer m.
Solution: Let a be the positive integer. According to Euclid’s division algorithm, $a=6q+r$, where the value of 0 ≤ r < 6 ${{a}^{2}}~={{\left( 6q+r \right)}^{2}}~=36{{q}^{2}}~+\text{...
Show that the square of any positive integer cannot be of the form 5q + 2 or 5q + 3 for any integer q.
Solution: Let ‘a’ be the positive integer According to Euclid’s division lemma, $a=bm+r$ The value of b is 5 according to the question, $a=5m+r$ So, r= 0, 1, 2, 3, 4 For r = 0,$a=5m$. For r =...
Show that cube of any positive integer is of the form 4m, 4m + 1 or 4m + 3, for some integer m.
Solution: Let any positive integer be ‘a’ and the value b is 4. According to Euclid Division Lemma, $a=bq+r$, where, 0 ≤ r < b $a=3q+r$, where, 0 ≤ r < 4 The possible values of ‘r’ according...
Show that the square of any positive integer is either of the form 4q or 4q + 1 for some integer q.
Solution: According to Euclid’s division lemma, $~a=bq+r$ According to the question, For b = 4. $a=4k+r$, 0 < r < 4 For r = 0, we obtain, $a=4k$...
A positive integer is of the form 3q + 1, q being a natural number. Can you write its square in any form other than 3m + 1, i.e., 3m or 3m + 2 for some integer m? Justify your answer.
Solution: No. Justification: Consider 3q + 1as the positive integer, where q is a natural number. (3q + 1)2 = 9q2 + 6q + 1 = 3(3q2 + 2q) + 1 = 3m + 1, (where m being an integer equals to 3q2 +...
Write whether the square of any positive integer can be of the form 3m + 2, where m is a natural number. Justify your answer.
Solution: No, the square of any positive integer cannot be of the form 3m + 2 where m is a natural number Justification: Applying the Euclid’s division lemma, The positive integer ‘a' can be written...
“The product of three consecutive positive integers is divisible by 6”. Is this statement true or false? Justify your answer.
Solution: Yes, the statement is true. Justification: Consider 2, 3, 4 as the three consecutive numbers \[\left( 2\text{ }\times \text{ }3\text{ }\times \text{ }4 \right)/6\text{ }=\text{ }24/6\text{...
“The product of two consecutive positive integers is divisible by 2”. Is this statement true or false? Give reasons.
Solution: Yes, the statement is true. Justification: Let ‘a’ and ‘a + 1’ be the two consecutive positive integers Applying the Euclid’s division lemma, We have, a = bq + r, where 0 ≤ r < b For...
Write whether every positive integer can be of the form 4q + 2, where q is an integer. Justify your answer.
Solution: No, every positive integer, where q is an integer cannot be of the form 4q + 2. Justification: All numbers in the form 4q + 2, where ‘q' is an integer, are even and not divisible by 4. For...
Choose the correct answer from the given four options in the following questions:
The largest number which divides 70 and 125, leaving remainders 5 and 8, respectively, is (A) 13 (B) 65 (C) 875 (D) 1750 Solution: Option(A) 13 Explanation: According to the question, Find the...
Choose the correct answer from the given four options in the following questions:
If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is: (A) 4 (B) 2 (C) 1 (D) 3 Solution: Option(B) 2 Explanation: Let's calculate the HCF of 65 and 117, 117 = 1×65 +...
Choose the correct answer from the given four options in the following questions:
n2 – 1 is divisible by 8, if n is: (A) an integer (B) a natural number (C) an odd integer (D) an even integer Solution: Option(C) an odd integer Explanation: Let x = n2 – 1 In the equation...
Choose the correct answer from the given four options in the following questions:
For some integer q, every odd integer is of the form: (A) q (B) q +1 (C) 2g (D) 2q +1 Solution: Option(D) i.e. 2q+1 Explanation: Those integers which are not divisible by 2 are odd integers. As a...
Choose the correct answer from the given four options in the following questions:
For some integer m, every even integer is of the form: (A) m (B) m +1 (C) 2m (D) 2m+1 Solution: Option(C) 2m Explanation: Those integers which are divisible by 2 are even integers. As a result, it...
12. Show that the square of any positive integer cannot be of the form 6m + 2 or 6m + 5 for any integer m.
Solution: Let the positive integer = a According to Euclid’s division algorithm, a = 6q + r, where 0 ≤ r < 6 \[{{a}^{2}}={{\left( 6q+r \right)}^{2}}=36{{q}^{2}}+{{r}^{2}}+12qr\],\[\because...
11. Show that any positive odd integer is of the form 6q +1 or 6q + 3 or 6q + 5, where q is some integer.
Let ‘a’ be any positive integer. Then from Euclid’s division lemma, a = bq+r; where 0 < r < b Putting b=6 we get, ⇒ a = 6q + r, 0 < r < 6 For r = 0, we get\[a=6q=2\left( 3q...
4. For any positive integer n, prove that n3 – n divisible by 6.
Let, n be any positive integer. And since any positive integer can be of the form 6q, or 6q+1, or 6q+2, or 6q+3, or 6q+4, or 6q+5. (From Euclid’s division lemma for b= 6) We have n3 – n =...
3. Prove that the product of three consecutive positive integers is divisible by 6.
Let n be any positive integer. Thus, the three consecutive positive integers are n, n+1 and n+2. We know that any positive integer can be of the form 6q, or...
Q.The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, p q what can you say about the prime factors of q?
(i) \[\mathbf{43}.\mathbf{123456789}\] (ii) \[\mathbf{0}.\mathbf{120120012000120000}\ldots \ldots \] $\left( III \right)$ $43.\overline{123456789}$ (i) \[\mathbf{43}.\mathbf{123456789}\] Since ,it...
Q.Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) ${}^{13}/{}_{3125}$ (ii) ${}^{17}/{}_{8}$ (iii) ${}^{64}/{}_{455}$ (iv) ${}^{15}/{}_{1600}$ (v) ${}^{29}/{}_{343}$ (vi)$23/{{2}^{3}}{{5}^{2}}$ (vii)...
Q.Prove that the following are irrationals?
$\left( 1 \right)$ ${}^{1}/{}_{\sqrt{2}}$ $(2)7\sqrt{5}$ $(3)6+\sqrt{2}$ $\left( 1 \right)$ Let us assume, ${}^{1}/{}_{\sqrt{2}}$ is rational. Then, we can find co-prime x and y$(y\ne 0)$ such that...
Q.Prove that 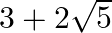 is irrational ?
is irrational ?
Let us assume $3+2\sqrt{5}$ is rational. Then we can find co-prime x and y($y\ne 0$ ) such that $3+2\sqrt{5}=\frac{x}{y}$ Rearranging , we get $2\sqrt{5}=\frac{x}{y}-3$...
Q.Prove that 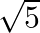 is irrational number?
is irrational number?
Let, $\sqrt{5}$ is rational number. Therefore ,$\sqrt{5}$ can be written as ${}^{x}/{}_{y}$ (where,x & y are coprime) $y\sqrt{5}=x$ Squaring both sides ${{(y\sqrt{5})}^{2}}={{x}^{2}}$ $$...
Q.There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Since, Both Sonia and Ravi move in the same direction and at the same time, The method to find the time when they will be meeting again at the starting point is LCM(Lowest Common Multiple) of 18...
Explain why 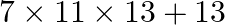 and
and  are composite numbers?
are composite numbers?
Numbers are of two types –prime numbers(two factors) & composite numbers(more then 2 factors). $(7\times 11\times 13)+13$ Taking 13 as common factor =$13[(7\times 11)+1]$ =$13(77+1)$...
Q. Check whether 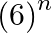 can end with the digit 0 for any natural number n?
can end with the digit 0 for any natural number n?
If last digit of any number is 0,it should be divisible by 10. It also divisible by 2 and 5 as $10=2\times 5$ Prime factorisation of ${{6}^{n}}={{(2\times 3)}^{n}}$ By observation we can say...
Q.Given that HCF (306, 657) = 9, find LCM (306, 657)?
As we know that, HCF×LCM=Product of the two given numbers(Multiplication of two given number) Since, HCF(Highest Common Factor) is given 9 of two numbers 306 & 657 Therefore using formula...
Q.Express each number as a product of its prime factors:
(i) 140 (ii) 156 (iii) 3825 (iv) 5005 (v) 7429 i) 140 By Taking the LCM(Lowest Common Multiple) of 140, we will get the product of its prime factor. Therefore, $140=2\times 2\times 5\times...
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Given, Number of army contingent members=616 Number of army band members = 32 When we find the HCF(616,32) then we get maximum number of columns in which they can march. We use Euclid’s...
Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Let a be any positive integer and b=6.Then,by Euclid’s algorithm, $a=6q+r$ for some integer $q\ge 0$ and r=0,1,2,3,4,5 because $0\le r<6$ . Therefore, $a=6q$ or $6q+1$ or $6q+2$ or $6q+3$...
Use Euclid’s division algorithm to find the HCF of:
(1)We have 225>135 So, we apply the division lemma to 225 & 135 to obtain 225=135×1+90 Here remainder 90≠0, we apply the division lemma again to 135 and 90 to obtain 135=90×1+45 We consider...
