Solution: (a) The length of perpendicular from the point $(2,3,-5)$ on the plane $x+2 y-2 z=9 \Rightarrow x+2 y-2 z-9=0$ is $\frac{\left|a x_{1}+b y_{1}+c z_{1}+d\right|}{\sqrt{a^{2}+b^{2}+c^{2}}}$...
In the following cases, find the distance of each of the given points from the corresponding given plane. Point Plane
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) 4x + 8y + z – 8 = 0 and y + z – 4 = 0
Solution: (a) $4 x+8 y+z-8=0$ and $y+z-4=0$ It is given that The eq. of the given planes are $4 x+8 y+z-8=0 \text { and } y+z-4=0$ It is known to us that, two planes are $\perp$ if the direction...
In the following cases, determine whether the given planes are parallel or perpendicular, and in case they are neither, find the angles between them.
(a) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
(b) 2x – 2y + 4z + 5 = 0 and 3x – 3y + 6z – 1 = 0
Solution: (a) $2 x-2 y+4 z+5=0$ and $3 x-3 y+6 z-1=0$ It is given that The eq. of the given planes are $2 x-2 y+4 z+5=0$ and $x-2 y+5=0$ It is known to us that, two planes are $\perp$ if the...
Find the equation of the plane through the line of intersection of the planes x + y + z = 1 and 2x + 3y + 4z = 5 which is perpendicular to the plane x – y + z = 0.
Solution: Let's say that the eq. of the plane that passes through the two-given planes $x+y+z=1$ and $2 x+3 y+4 z=5$ is $\begin{array}{l} (x+y+z-1)+\lambda(2 x+3 y+4 z-5)=0 \\ (2 \lambda+1) x+(3...
Find the equation of the plane through the intersection of the planes 3x – y + 2z – 4 = 0 and x + y + z – 2 = 0 and the point (2, 2, 1).
Solution: It is given that Eq. of the plane passes through the intersection of the plane is given by $(3 x-y+2 z-4)+\lambda(x+y+z-2)=0$ and the plane passes through the points $(2,2,1)$ Therefore,...
Find the equation of the plane with intercept 3 on the  -axis and parallel to ZOX plane.
-axis and parallel to ZOX plane.
Solution: It is known to us that the equation of the plane $\mathrm{ZOX}$ is $\mathrm{y}=0$ Therefore, the equation of plane parallel to $\mathrm{ZOX}$ is of the form, $\mathrm{y}=\mathrm{a}$ As the...
Find the equations of the planes that passes through three points.
(a) (1, 1, –1), (6, 4, –5), (–4, –2, 3)
(b) (1, 1, 0), (1, 2, 1), (–2, 2, –1)
Solution: (a) It is given that, The points are $(1,1,-1),(6,4,-5),(-4,-2,3)$. Let, $\begin{array}{l} =\left|\begin{array}{ccc} 1 & 1 & -1 \\ 6 & 4 & -5 \\ -4 & -2 & 3...
Find the Cartesian equation of the following planes:
(a) 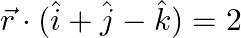
(b) 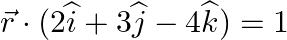
Solution: (a) It is given that, The equation of the plane. Let $\overrightarrow{\mathrm{r}}$ be the position vector of $\mathrm{P}(\mathrm{x}, \mathrm{y}, \mathrm{z})$ is given by $\vec{r}=x...
In each of the following cases, determine the direction cosines of the normal to the plane and the distance from the origin.
(a) 2x + 3y – z = 5
(b) 5y + 8 = 0
Solution: (a) $2 x+3 y-z=5$ It is given that The eq. of the plane, $2 x+3 y-z=5 \ldots$. (1) The direction ratio of the normal $(2,3,-1)$ Using the formula,...
Find the shortest distance between the lines whose vector equations are 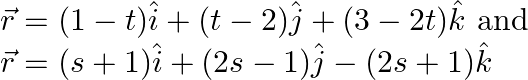
Solution: Consider the given equations $\begin{array}{l} \Rightarrow \vec{r}=(1-t) \hat{i}+(t-2) \hat{j}+(3-2 t) \hat{k} \\ \vec{r}=\hat{i}-t \hat{i}+t \hat{j}-2 \hat{j}+3 \hat{k}-2 t \hat{k} \\...
Find the shortest distance between the lines 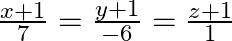 and
and 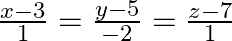
Solution: It is known to us that the shortest distance between two lines $\frac{x+1}{7}=\frac{y+1}{-6}=\frac{z+1}{1}$ and $\frac{x-3}{1}=\frac{y-5}{-2}=\frac{z-7}{1}$ is given as:...
Show that the lines 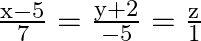 and
and 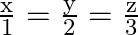 are perpendicular to each other.
are perpendicular to each other.
Solution: The equations of the given lines are $\frac{\mathrm{x}-5}{7}=\frac{\mathrm{y}+2}{-5}=\frac{\mathrm{z}}{1}$ and $\frac{\mathrm{x}}{1}=\frac{\mathrm{y}}{2}=\frac{\mathrm{z}}{3}$ Two lines...
Find the values of p so that the lines 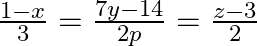 and
and 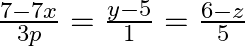 are at right angles.
are at right angles.
Solution: The standard form of a pair of Cartesian lines is:...
Find the vector and the Cartesian equations of the line that passes through the points (3, –2, –5), (3, –2, 6).
Solution: It is given that Let's calculate the vector form: The vector eq. of as line which passes through two points whose position vectors are $\vec{a}$ and $\vec{b}$ is...
Find the vector and the Cartesian equations of the lines that passes through the origin and (5, –2, 3).
Solution: Given: The origin $(0,0,0)$ and the point $(5,-2,3)$ It is known to us that The vector eq. of as line which passes through two points whose position vectors are $\vec{a}$ and $\vec{b}$ is...
Find the Cartesian equation of the line which passes through the point 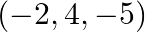 and parallel to the line given by
and parallel to the line given by 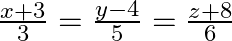
Solution: It is given that The points $(-2,4,-5)$ It is known that Now, the Cartesian equation of a line through a point $\left(\mathrm{x}_{1}, \mathrm{y}_{1}, \mathrm{z}_{1}\right)$ and having...
Find the equation of the line which passes through the point (1, 2, 3) and is parallel to the vector 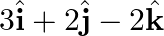
Solution: Given that, Line passes through the point $(1,2,3)$ and is parallel to the vector. It is known to us that Vector eq. of a line that passes through a given point whose position vector is...
Show that the line through the points (4, 7, 8), (2, 3, 4) is parallel to the line through the points (–1, –2, 1), (1, 2, 5).
Solution: The points $(4,7,8),(2,3,4)$ and $(-1,-2,1),(1,2,5)$. Consider $A B$ be the line joining the points, $(4,7,8),(2,3,4)$ and $C D$ be the line through the points $(-1,-2$, 1), $(1,2,5)$. So...
Show that the line through the points (1, –1, 2), (3, 4, –2) is perpendicular to the line through the points (0, 3, 2) and (3, 5, 6).
Solution: Given that The points $(1,-1,2),(3,4,-2)$ and $(0,3,2),(3,5,6)$. Let's consider $A B$ be the line joining the points, $(1,-1,2)$ and $(3,4,-2)$, and $C D$ be the line through the points...
