Login/Sign Up
Home » Examine the applicability of Mean Value Theorem for all the three functions being given below: [Note for students: Check exercise 2] (i) for (ii) for
Examine the applicability of Mean Value Theorem for all the three functions being given below: [Note for students: Check exercise 2] (i) f(x)=[x] for x \in[5,9] (ii) f(x)=[x] for x \in[-2,2]
CBSE | Class 12 | Continuity and Differentiability | Exercise 5.8 | Maths | NCERT
Examine the applicability of Mean Value Theorem for all the three functions being given below: [Note for students: Check exercise 2] (i) f(x)=[x] for x \in[5,9] (ii) f(x)=[x] for x \in[-2,2]

Solution:

As per the Mean Value Theorem :

For a given function f:[a, b] \rightarrow R, if

(a) f is continuous on (a, b)

(b) f is differentiable on (a, b)

Therefore there exist some c \in(a, b) such that f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}

(i) f(x)=[x] for x \in[5,9]

Provided function f(x) is not continuous at x=5 and x=9.

As a result, f(x) is not continuous at [5,9].

Let n be an integer such that n \in[5,9]

\therefore Left Hand Limit = \lim _{h \rightarrow 0} \frac{f(n+h)-f(n)}{h}=\lim _{h \rightarrow 0^{-}} \frac{(n+h)-(n)}{h}=\lim _{h \rightarrow 0^{-}} \frac{n-1-n}{h}=\lim _{h \rightarrow 0} \frac{-1}{h}=\infty

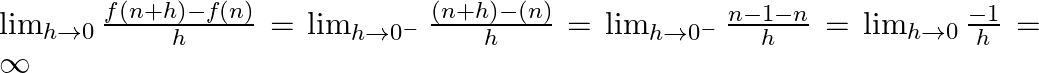
And Right Hand Limit = \lim _{h \rightarrow 0^{-}} \frac{f(n+h)-f(n)}{h}=\lim _{h \rightarrow 0^{-}} \frac{(n+h)-(n)}{h}=\lim _{h \rightarrow 0^{-}} \frac{n-n}{h}=\lim _{h \rightarrow 0^{-}} 0=0

As, L.H.L. \neq R.H.L.,

Hence f is not differentiable at [5,9].

As a result, M.V.T. is not applicable for this function.

(ii) f(x)=[x] for x \in[-2,2]

The provided function f(x) is not continuous at x=-2 and x=2.

Then, f(x) is not continuous at [-2,2].

Let n be an integer such that n \in[-2,2]

\therefore Left Hand Limit = \lim _{h \rightarrow 0} \frac{f(n+h)-f(n)}{h}=\lim _{h \rightarrow 0^{-}} \frac{(n+h)-(n)}{h}=\lim _{n \rightarrow 0^{-}} \frac{n-1-n}{h}=\lim _{h \rightarrow 0} \frac{-1}{h}=\infty

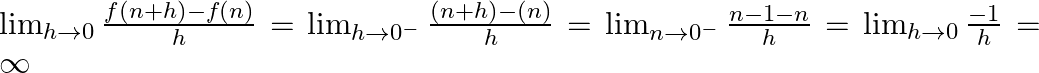
And Right Hand Limit = \lim _{h \rightarrow 0^{-}} \frac{f(n+h)-f(n)}{h}=\lim _{h \rightarrow 0^{-}} \frac{(n+h)-(n)}{h}=\lim _{h \rightarrow 0^{-}} \frac{n-n}{h}=\lim _{h \rightarrow 0^{-}} 0=0

As, L.H.L. \neq R.H.L.,

As a result, f is not differentiable at [-2,2].

i

More Material