$2 x^{2}+x+4=0$ $\Rightarrow 4 x^{2}+2 x+8=0 \quad$ (Multiplying both sides by 2) $\Rightarrow 4 x^{2}+2 x=-8$ $\Rightarrow(2 x)^{2}+2 \times 2 x \times...
By using the method of completing the square, show that the equation
Solve the following quadratic equations: (xi) 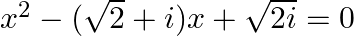 (xii)
(xii) 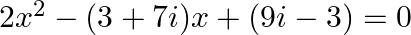
(xi) $x^{2}-(\sqrt{2}+i) x+\sqrt{2 i}=0$ $x^{2}-(\sqrt{2 x}+i x)+\sqrt{2 i}=0$ $x^{2}-\sqrt{2 x}-i x+\sqrt{2 i}=0$ $x(x-\sqrt{2})-i(x-\sqrt{2})=0$ $(x-\sqrt{2})(x-i)=0$ $(x-\sqrt{2})=0$ or $(x-i)=0$...
Solve the following quadratic equations: (ix) 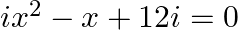 (x)
(x) 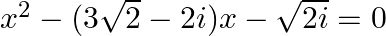
(ix) $i x^{2}-x+12 i=0$ $i x^{2}+x(-1)+12 i=0\left[\right.$ We know, $\left.i^{2}=-1\right]$ substituting $-1=\mathrm{i}^{2}$ $\mathrm{ix}^{2}+\mathrm{xi}^{2}+12 \mathrm{i}=0$...
Solve the following quadratic equations: (vii) 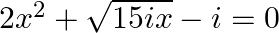 (viii)
(viii) 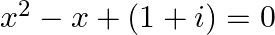
(vii) 2x2 + √15ix – i = 0 applying discriminant rule, x = (-b ±√(b2 – 4ac))/2a a = 2, b = √15i, c = -i =>15 – 8i = 16 – 1 – 8i 15 – 8i = 16 + (–1) – 8i = 16 + i2 – 8i [∵ i2 = –1] = 42 + (i)2 –...
Solve the following quadratic equations: (v) 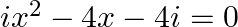 (vi)
(vi) 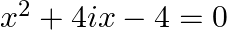
(v) $i x^{2}-4 x-4 i=0$ $i x^{2}+4 x(-1)-4 i=0\left[W\right.$ e know, $\left.i^{2}=-1\right]$ substituting $-1=\mathrm{i}^{2}$ $\mathrm{ix}^{2}+4 \mathrm{xi}^{2}-4 \mathrm{i}=0$ $i\left(x^{2}+4 i...
Solve the following quadratic equations: (iii) 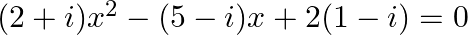 (iv)
(iv) 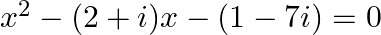
(iii) (2 + i)x2 – (5- i)x + 2 (1 – i) = 0 applying discriminant rule, x = (-b ±√(b2 – 4ac))/2a a = (2+i), b = -(5-i), c = 2(1-i) since, i2 = –1 substituting –1 = i2 x = (1 – i) or 4/5 – 2i/5 ∴ The...
Solve the following quadratic equations: (i) 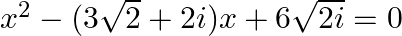 (ii)
(ii) 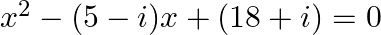
(i) $x^{2}-(3 \sqrt{2}+2 i) x+6 \sqrt{2} i=0$ $x^{2}-(3 \sqrt{2} x+2 i x)+6 \sqrt{2 i}=0$ $x^{2}-3 \sqrt{2 x}-2 i x+6 \sqrt{2 i}=0$ $x(x-3 \sqrt{2})-2 i(x-3 \sqrt{2})=0$ $(x-3 \sqrt{2})(x-2 i)=0$...
Solving the following quadratic equations by factorization method: (iii) 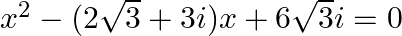 (iv)
(iv) 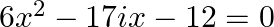
(iii) $x^{2}-(2 \sqrt{3}+3 i) x+6 \sqrt{3} i=0$ $x^{2}-(2 \sqrt{3} x+3 i x)+6 \sqrt{3} i=0$ $x^{2}-2 \sqrt{3} x-3 i x+6 \sqrt{3} i=0$ $x(x-2 \sqrt{3})-3 i(x-2 \sqrt{3})=0$ $(x-2 \sqrt{3})(x-3 i)=0$...
Solving the following quadratic equations by factorization method: (i) 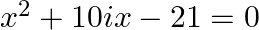 (ii)
(ii) 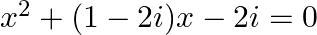
(i) $x^{2}+10 i x-21=0$ $x^{2}+10 i x-21 \times 1=0$ since, $i^{2}=-1 \Rightarrow 1=-\mathrm{i}^{2}$ substituting $1=-\mathrm{i}^{2}$ $x^{2}+10 i x-21\left(-i^{2}\right)=0$ $x^{2}+10 i x+21...
Solve the following quadratic equations by factorization method only: 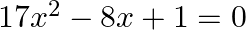
$17 x^{2}-8 x+1=0$ applying discriminant rule, $x=\left(-b \pm \sqrt{\left.\left(b^{2}-4 a c\right)\right) / 2 a}\right.$ $a=17, b=-8, c=1$ $\mathrm{x}=\left(-(-8) \pm...
Solve the following quadratic equations by factorization method only: 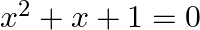
$x^{2}+x+1=0$ $x^{2}+x+1 / 4+3 / 4=0$ $x^{2}+2(x)(1 / 2)+(1 / 2)^{2}+3 / 4=0$ $(x+1 / 2)^{2}+3 / 4=0\left[\right.$ Since, $\left.(a+b)^{2}=a^{2}+2 a b+b^{2}\right]$ $(x+1 / 2)^{2}+3 / 4 \times 1=0$...
Solve the following quadratic equations by factorization method only: 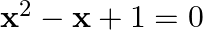
$x^{2}-x+1=0$ $x^{2}-x+1 / 4+3 / 4=0$ $x^{2}-2(x)(1 / 2)+(1 / 2)^{2}+3 / 4=0$ $(x-1 / 2)^{2}+3 / 4=0\left[\right.$ Since, $\left.(a+b)^{2}=a^{2}+2 a b+b^{2}\right]$ $(x-1 / 2)^{2}+3 / 4 \times 1=0$...
Solve the following quadratic equations by factorization method only: 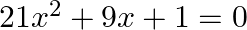
$21 \mathrm{x}^{2}+9 \mathrm{x}+1=0$ applying discriminant rule, Where, $x=\left(-b \pm \sqrt{\left.\left(b^{2}-4 a c\right)\right) / 2 a}\right.$ $a=21, b=9, c=1$ $\left.x=\left(-9 \pm...
Solve the following quadratic equations by factorization method only: 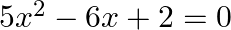
$5 x^{2}-6 x+2=0$ applying discriminant rule, where, $x=\left(-b \pm \sqrt{\left.\left(b^{2}-4 a c\right)\right) / 2 a}\right.$ $a=5, b=-6, c=2$ => $\left.x=\left(-(-6) \pm...
Solve the following quadratic equations by factorization method only: 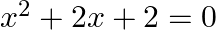
$x^{2}+2 x+2=0$ $x^{2}+2 x+1+1=0$ $x^{2}+2(x)(1)+1^{2}+1=0$ $(x+1)^{2}+1=0\left[\because(a+b)^{2}=a^{2}+2 a b+b^{2}\right]$ $\mathrm{since}, \mathrm{i}^{2}=-1 \Rightarrow 1=-\mathrm{i}^{2}$...
Solve the following quadratic equations by factorization method only: 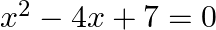
$x^{2}-4 x+7=0$ $x^{2}-4 x+4+3=0$ $x^{2}-2(x)(2)+2^{2}+3=0$ $(x-2)^{2}+3=0\left[\right.$ Since, $\left.(a-b)^{2}=a^{2}-2 a b+b^{2}\right]$ $(x-2)^{2}+3 \times 1=0$ since, $\mathrm{i}^{2}=-1...
Solve the following quadratic equations by factorization method only: 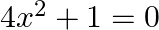
$4 \mathrm{x}^{2}+1=0$ Since, $i^{2}=-1 \Rightarrow 1=-\mathrm{i}^{2}$ substituting $1=-\mathrm{i}^{2}$ in the above equation, we get $4 x^{2}-i^{2}=0$ $(2 x)^{2}-i^{2}=0$...
Solve the following quadratic equations by factorization method only: 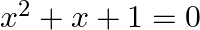
$\mathrm{x}^{2}+\mathrm{x}+1=0$ $x^{2}+x+1 / 4+3 / 4=0$ $x^{2}+2(x)(1 / 2)+(1 / 2)^{2}+3 / 4=0$ $(x+1 / 2)^{2}+3 / 4=0\left[\right.$ Since, $\left.(a+b)^{2}=a^{2}+2 a b+b^{2}\right]$ $(x+1 /...
Solve the following quadratic equations by factorization method only: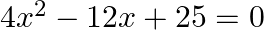
$4 x^{2}-12 x+25=0$ $4 x^{2}-12 x+9+16=0$ $(2 x)^{2}-2(2 x)(3)+3^{2}+16=0$ $(2 x-3)^{2}+16=0\left[\right.$ Since, $\left.(a+b)^{2}=a^{2}+2 a b+b^{2}\right]$ $(2 x-3)^{2}+16 \times 1=0$...
Solve the following quadratic equations by factorization method only: 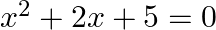
$x^{2}+2 x+5=0$ $x^{2}+2 x+1+4=0$ $x^{2}+2(x)(1)+1^{2}+4=0$ $(x+1)^{2}+4=0\left[\right.$ since, $\left.(a+b)^{2}=a^{2}+2 a b+b^{2}\right]$ $(x+1)^{2}+4 \times 1=0$ Since, $i^{2}=-1 \Rightarrow...
Solve the following quadratic equations by factorization method only :9x^2 + 4 = 0
$9 x^{2}+4=0$ $9 x^{2}+4 \times 1=0$ Since, $\dot{i}^{2}=-1 \Rightarrow 1=-\mathrm{i}^{2}$ substituting $1=-\mathrm{i}^{2}$ $9 x^{2}+4\left(-i^{2}\right)=0$ $9 x^{2}-4 i^{2}=0$ $(3 x)^{2}-(2...
Solve the following quadratic equations by factorization method only: x^2 + 1 = 0
\[\begin{array}{*{35}{l}} {{x}^{2}}~+\text{ }1\text{ }=\text{ }0 \\ Since,\text{ }{{i}^{2}}~=\text{ }-1~\Rightarrow ~1\text{ }=\text{ }-{{i}^{2}} \\ ~substituting\text{ }1\text{ }=\text{...
