From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants. (a) $3 \mathrm{NO}(g) \rightarrow \mathrm{N}_{2} \mathrm{O}(g)$ Rate $=\mathrm{k}[\mathrm{NO}]^{2}$ (b) $\mathrm{H}_{2} \mathrm{O}_{2}(a q)+3 \mathrm{I}^{-}(a q)+2 \mathrm{H}^{+} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(I)+\mathrm{I}_{3}^{-}$Rate $=\mathrm{k}\left[\mathrm{H}_{2} \mathrm{O}_{2}\right]\left[\mathrm{I}^{-}\right]$ (c) $\mathrm{CH}_{3} \mathrm{CHO}(g) \rightarrow \mathrm{CH}_{4}(g)+\mathrm{CO}(g)$ Rate $=\mathrm{k}\left[\mathrm{CH}_{3} \mathrm{CHO}\right]^{\frac{3}{2}}$ (d) $\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{Cl}(g) \rightarrow \mathrm{C}_{2} \mathrm{H}_{4}(g)+\mathrm{HCl}(g)$ Rate $=\mathrm{k}\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{Cl}\right]$

From the rate expression for the following reactions, determine their order of reaction and the dimensions of the rate constants.
(a) $3 \mathrm{NO}(g) \rightarrow \mathrm{N}_{2} \mathrm{O}(g)$ Rate $=\mathrm{k}[\mathrm{NO}]^{2}$
(b) $\mathrm{H}_{2} \mathrm{O}_{2}(a q)+3 \mathrm{I}^{-}(a q)+2 \mathrm{H}^{+} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(I)+\mathrm{I}_{3}^{-}$ Rate $=\mathrm{k}\left[\mathrm{H}_{2} \mathrm{O}_{2}\right]\left[\mathrm{I}^{-}\right]$
(c) $\mathrm{CH}_{3} \mathrm{CHO}(g) \rightarrow \mathrm{CH}_{4}(g)+\mathrm{CO}(g)$ Rate $=\mathrm{k}\left[\mathrm{CH}_{3} \mathrm{CHO}\right]^{\frac{3}{2}}$ (d) $\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{Cl}(g) \rightarrow \mathrm{C}_{2} \mathrm{H}_{4}(g)+\mathrm{HCl}(g)$ Rate $=\mathrm{k}\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{Cl}\right]$

Chemistry | Previous year Chemistry Question Paper | Previous Year Question Papers

Solution:
(a) Given rate $=k[N O]^{2}$
Therefore, order of the reaction $=2$
Dimensions of $k=\frac{\text { Rete }}{[N O]^{\sharp}}$

$\begin{array}{l} =\frac{\operatorname{mal} L^{-1} \mathrm{~s}^{-1}}{\left(\mathrm{~mol} L^{-1}\right)^{2}} \\ =\frac{\operatorname{mol} L^{-1} \mathrm{~s}^{-1}}{\operatorname{mol}^{-2} L^{-1}} \\ =L \mathrm{~mol}^{-1} \mathrm{~s}^{-1} \end{array}$

(b) Given rate $=k\left[\mathrm{H}_{2} \mathrm{O}_{2}\right]\left[\mathrm{I}^{-}\right]$
Therefore, order of the reaction $=2$
Dimensions of $k=\frac{R a t e}{\left.\left[H_{2} O_{2}\right] I^{-}\right]}$

$\begin{array}{l} =\frac{m o l}{\left(\operatorname{mol} L^{-1}\right)\left(\operatorname{mol} L^{-1}\right)} \\ =L m o l^{-1} s^{-1} \end{array}$

(c) Given rate $=k\left[\mathrm{CH}_{3} \mathrm{CHO}\right]^{\frac{1}{2}}$
Therefore, the order of reaction $=\frac{3}{2}$
Chemical Kinetics
Dimensions of 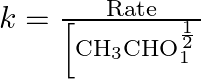$k=\frac{\text { Rate }}{\left[\mathrm{CH}_{3} \mathrm{CHO}_{1}^{\frac{1}{2}}\right.}$
$=\frac{m o l}{\left(m o l^{-1} z^{-1}\right)^{\frac{2}{2}}}$ $=\frac{m o l}{m o l^{-1} \frac{1}{2}-1^{\frac{1}{2}}}$ $L^{\frac{1}{2}} m o l^{-\frac{1}{2}} s^{-1}$
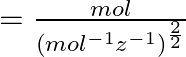
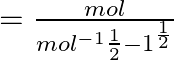
(d) Given rate $=\mathrm{k}=\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{Cl}\right]$
Therefore, order of the reaction $=1$
Dimension of $k=\frac{\text { Rote }}{\left[\mathrm{C}_{2} \mathrm{H}_{5} \mathrm{Cl}\right.}$