![]()
![]()
![]()
![]()
![]()
![]()
Solution:
Given
![]()
![]()
Cross multiplication Method
![Rendered by QuickLaTeX.com \[\frac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\frac{-y}{{{a}_{1}}{{c}_{2}}-{{a}_{2}}{{c}_{1}}}=\frac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-007fa7175ae1f5c3950c34825b73ca25_l3.png)
Comparing the two equations
![Rendered by QuickLaTeX.com \[{{a}_{1}}=\frac{1}{a},\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0200af07ee6824a6ff78430e31a62a20_l3.png)
![Rendered by QuickLaTeX.com \[{{b}_{1}}=\frac{1}{b},\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-56d1bd0abec514d7269b0a3c51ec9544_l3.png)
![]()
![Rendered by QuickLaTeX.com \[{{a}_{2}}=\frac{1}{{{a}^{2}}},{{b}_{2}}=\frac{1}{{{b}^{2}}},{{c}_{2}}=-2\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d8b4119d8123fa4bb0f05f5dcb73ff73_l3.png)
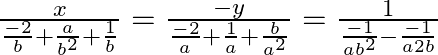
![Rendered by QuickLaTeX.com \[\frac{x}{\frac{a-b}{{{b}^{2}}}}=\frac{-y}{\frac{-a-b}{{{a}^{2}}}+\frac{1}{a}+\frac{b}{{{a}^{2}}}}=\frac{1}{\frac{-1}{a{{b}^{2}}}-\frac{-1}{a2b}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d84b296d4b18e54350200a5d933ea8ae_l3.png)
![Rendered by QuickLaTeX.com \[\frac{x}{\frac{a-b}{{{b}^{2}}}}=\frac{1}{\frac{-1}{a{{b}^{2}}}-\frac{-1}{a2b}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-f055bafb967ecb52ff7076545b7a9b56_l3.png)
![]()
![Rendered by QuickLaTeX.com \[\frac{-y}{\frac{-a-b}{{{a}^{2}}}+\frac{1}{a}+\frac{b}{{{a}^{2}}}}=\frac{1}{\frac{-1}{a{{b}^{2}}}-\frac{-1}{a2b}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-8cb8acdbfc6941cb2eb83a5fa0388713_l3.png)
![]()
![]() and
and ![]()
Solution:
Given
![]()
![]()
Cross multiplication Method
![Rendered by QuickLaTeX.com \[\frac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\frac{-y}{{{a}_{1}}{{c}_{2}}-{{a}_{2}}{{c}_{1}}}=\frac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-007fa7175ae1f5c3950c34825b73ca25_l3.png)
Comparing the two equations
![Rendered by QuickLaTeX.com \[{{a}_{1}}=\frac{1}{a},\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-0200af07ee6824a6ff78430e31a62a20_l3.png)
![Rendered by QuickLaTeX.com \[{{b}_{1}}=\frac{1}{b},\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-56d1bd0abec514d7269b0a3c51ec9544_l3.png)
![]()
![]()
![]()
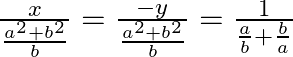
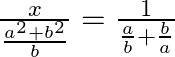
=![]()
And,
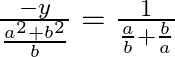
=![]()
![]() and
and ![]()
