Solution: Option(A) is correct. To Find: The range of $\cos ^{-1} x$ Here, the inverse function is given by $\mathrm{y}=\mathrm{f}^{-1}(x)$ The graph of the function $y=\cos ^{-1}(x)$ can be...
Mark the tick against the correct answer in the following: Range of
Mark the tick against the correct answer in the following: Range of 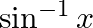 is
is
A. ![Rendered by QuickLaTeX.com \left[0, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-cdf7f72b896a3c8ef3745557ca17a3c9_l3.png)
B. ![Rendered by QuickLaTeX.com [0, \pi]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-3ee8a7f2b7324e2152a4807a1b912cfc_l3.png)
C. ![Rendered by QuickLaTeX.com \left[\frac{-\pi}{2}, \frac{\pi}{2}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-d03f7933dddf8dbceee8c92c85707a25_l3.png)
D. None of these
Solution: Option() is correct. To Find: The range of $\sin ^{-1} x$ Here,the inverse function is given by $\mathrm{y}=\mathrm{f}^{-1}(x)$ The graph of the function $y=\sin ^{-1}(x)$ can be obtained...
Mark the tick against the correct answer in the following: 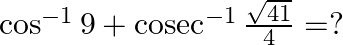
A. 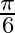
B. 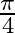
C. 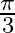
D. 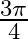
Solution: Option(B) is correct. To Find: The value of $\cot ^{-1} 9+\operatorname{cosec}^{-1} \frac{\sqrt{41}}{4}$ Now $\cot ^{-1} 9+\operatorname{cosec}^{-1} \frac{\sqrt{41}}{4}$ can be written in...
Mark the tick against the correct answer in the following: 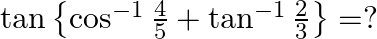
A. 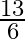
B. 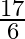
C. 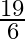
D. 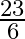
Solution: Option(B) is correct. To Find: The value of $\tan \left\{\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}\right\}$ Let $x=\cos ^{-1} \frac{4}{5}$ $\Rightarrow \cos x=\frac{4}{5}=\frac{\text {...
Mark the tick against the correct answer in the following: If 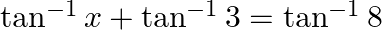 then
then 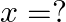
A. 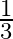
B. 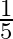
C. 3
D. 5
Solution: Option(B) is correct. Given: $\tan ^{-1} x+\tan ^{-1} 3=\tan ^{-1} 8$ To Find: The value of $x$ Here $\tan ^{-1} x+\tan ^{-1} 3=\tan ^{-1} 8$ can be written as $\tan ^{-1} x=\tan ^{-1}...
If 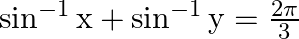 then
then 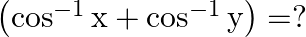
A. 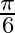
B. 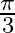
C. 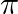
D. 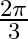
Solution: Option(B) is correct. Given: $\sin ^{-1} x+\sin ^{-1} y=\frac{2 \pi}{3}$ To Find: The value of $\cos ^{-1} x+\cos ^{-1} y$ Since we know that $\sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}$...
Mark the tick against the correct answer in the following: If 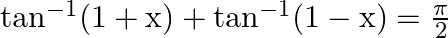 then
then 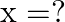
A. 1
B. 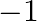
C. 0
D. 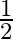
Solution: Option(C) is correct. To Find: The value of $\tan ^{-1}(1+x)+\tan ^{-1}(1-x)=\frac{\pi}{2}$ Since we know that $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$...
Mark the tick against the correct answer in the following: If 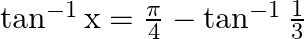 then
then 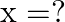
A. 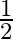
B. 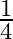
C. 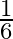
D. None of these
Solution: Option(A) is correct. To Find: The value of $\tan ^{-1} x=\frac{\pi}{4}-\tan ^{-1} \frac{1}{3}$ Now, $\tan ^{-1} x=\tan ^{-1} 1-\tan ^{-1} \frac{1}{3}\left(\because \tan...
Mark the tick against the correct answer in the following: ![Rendered by QuickLaTeX.com \sin \left[2 \tan ^{-1} \frac{5}{8}\right]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-111a4736820b38750893122ca95b27ed_l3.png)
A. 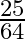
B. 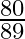
C. 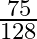
D. none of these
Solution: Option(B) is correct. To Find: The value of $\sin \left(2 \tan ^{-1} \frac{5}{8}\right)$ Let, $x=\sin \left(2 \tan ^{-1} \frac{5}{8}\right)$ We know that $2 \tan ^{-1} x=\sin...
Mark the tick against the correct answer in the following: 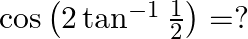
A. 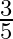
B. 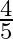
C. 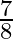
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cos \left(2 \tan ^{-1} \frac{1}{2}\right)$ Let, $x=\cos \left(2 \tan ^{-1} \frac{1}{2}\right)$ $\Rightarrow \mathrm{x}=\cos \left(\tan ^{-1}...
Mark the tick against the correct answer in the following: 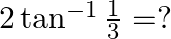
A. 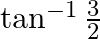
B. 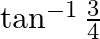
C. 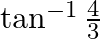
D. none of these
Solution: Option(B) is correct. To Find: The value of $2 \tan ^{-1} \frac{1}{3}$ i.e, $\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{3}$ Let, $x=\tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{3}$ Since we...
Mark the tick against the correct answer in the following: 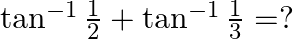
A. 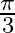
B. 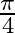
C. 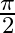
D. 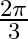
Solution: Option(B) is correct. To Find: The value of $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}$ Let, $x=\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}$ Since we know that $\tan ^{-1} x+\tan...
Mark the tick against the correct answer in the following: 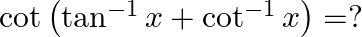
A. 1
B. 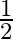
C. 0
D. none of these
Solution: Option(C) is correct. To Find: The value of $\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)$ Let, $x=\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)$ $\begin{array}{l} \Rightarrow \mathrm{x}=\cot...
Mark the tick against the correct answer in the following: 
A. 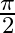
B. 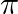
C. 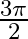
D. none of these
Solution: Option(C) is correct. To Find: The value of $\sin ^{-1}\left(\frac{-1}{2}\right)+2 \cos ^{-1}\left(\frac{-\sqrt{3}}{2}\right)$ Let, $x=\sin ^{-1}\left(\frac{-1}{2}\right)+2 \cos...
Mark the tick against the correct answer in the following: If 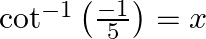 then
then 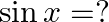
A. 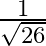
B. 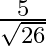
C. 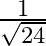
D. none of these
Solution: Option(B) is correct. Given: $\cot ^{-1} \frac{-1}{5}=x$ To Find: The value of $\sin \mathrm{x}$ Since, $x=\cot ^{-1} \frac{-1}{5}$ $\Rightarrow \cot \mathrm{x}=\frac{-1}{5}=\frac{\text {...
Mark the tick against the correct answer in the following: 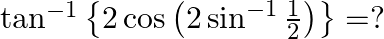
A. 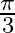
B. 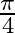
C. 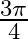
D. 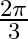
Solution: Option(B) is correct. To Find: The value of $\tan ^{-1}\left\{2 \cos \left(2 \sin ^{-1} \frac{1}{2}\right)\right\}$ Let, $x=\tan ^{-1}\left\{2 \cos \left(2 \sin ^{-1}...
Mark the tick against the correct answer in the following: 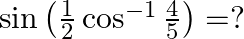
A. 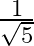
B. 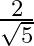
C. 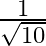
D. 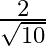
Solution: Option(C) is correct. To Find: The value of $\sin \left(\frac{1}{2} \cos ^{-1} \frac{4}{5}\right)$ Let $x=\cos ^{-1} \frac{4}{5}$ $\Rightarrow \cos x=\frac{4}{5}$ Therefore $\sin...
Mark the tick against the correct answer in the following: 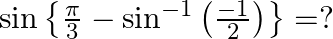
A. 1
B. 0
C. 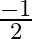
D. none of these
Solution: Option(A) is correct. To Find: The value of of $\sin \left\{\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right\}$ Let, $x=\sin \left\{\frac{\pi}{3}-\sin...
Mark the tick against the correct answer in the following: 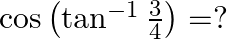
A. 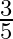
B. 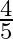
C. 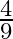
D. none of these
Solution: Option(B) is correct. To Find: The value of $\cos \left(\tan ^{-1} \frac{3}{4}\right)$ Let $x=\tan ^{-1} \frac{3}{4}$ $\begin{array}{l} \Rightarrow \tan x=\frac{3}{4} \\ \Rightarrow \tan...
Mark the tick against the correct answer in the following: 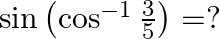
A. 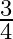
B. 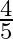
C. 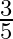
D. none of these
Solution: Option(B) is correct. To Find: The value of $\sin \left(\cos ^{-1} \frac{3}{5}\right)$ Let, $x=\cos ^{-1} \frac{3}{5}$ $\Rightarrow \cos x=\frac{3}{5}$ Now, $\sin \left(\cos ^{-1}...
Mark the tick against the correct answer in the following: 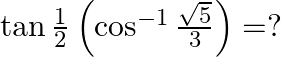
A. 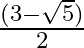
B. 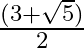
C. 
D. 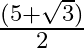
Solution: Option(A) is correct. To Find: The value of $\tan \frac{1}{2}\left(\cos ^{-1} \frac{\sqrt{5}}{3}\right)$ Let, $x=\cos ^{-1} \frac{\sqrt{5}}{3}$ $\Rightarrow \cos x=\frac{\sqrt{5}}{3}$ Now,...
Mark the tick against the correct answer in the following: ![Rendered by QuickLaTeX.com \tan \left[2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right]=?](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-7b682318a7b83adde969470e6e4ef16e_l3.png)
A. 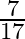
B. 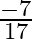
C. 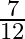
D. 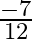
Solution: Option(B) is correct. To Find: The value of $\tan \left(2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right)$ Consider, $\tan \left(2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right)=\tan \left(\tan...
Mark the tick against the correct answer in the following: 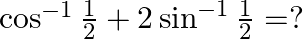
A. 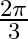
B. 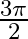
C. 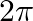
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cos ^{-1} \frac{1}{2}+2 \sin ^{-1} \frac{1}{2}$ Now, let $x=\cos ^{-1} \frac{1}{2}+2 \sin ^{-1} \frac{1}{2}$ $\Rightarrow...
Mark the tick against the correct answer in the following: 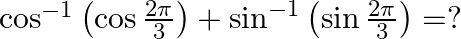
A. 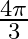
B. 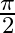
C. 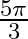
D. 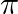
Solution: Option(D) is correct. To Find: The value of $\cos ^{-1}\left(\cos \left(\frac{2 \pi}{3}\right)\right)+\sin ^{-1}\left(\sin \left(\frac{2 \pi}{3}\right)\right)$ Here, consider $\cos...
Mark the tick against the correct answer in the following: If 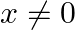 then
then 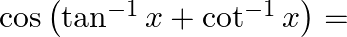 ?
?
A. 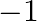
B. 1
C. 0
D. none of these
Solution: Option(C) is correct. Given: $x \neq 0$ To Find: The value of $\cos \left(\tan ^{-1} x+\cot ^{-1} x\right)$ Now, let $x=\cos \left(\tan ^{-1} x+\cot ^{-1} x\right)$ $\begin{array}{l}...
Mark the tick against the correct answer in the following: The value of 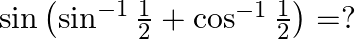
A. 0
B. 1
C. 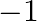
D. none of these
Solution: Option(1) is correct. To Find: The value of $\sin \left(\sin ^{-1} \frac{1}{2}+\cos ^{-1} \frac{1}{2}\right)$ Now, let $x=\sin \left(\sin ^{-1} \frac{1}{2}+\cos ^{-1} \frac{1}{2}\right)$...
Mark the tick against the correct answer in the following: 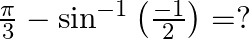
A. 0
B. 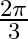
C. 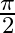
D. 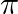
Solution: Option(D) is correct. To Find: The value of $\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)$ Now, let $x=\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)$ $\begin{array}{l} \Rightarrow...
Mark the tick against the correct answer in the following: The value of 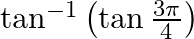 is
is
A. 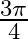
B. 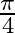
C. 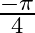
D. none of these
Solution: Option(C) is correct. To Find: The value of $\tan ^{-1}\left(\tan \left(\frac{3 \pi}{4}\right)\right)$ Now, let $x=\tan ^{-1}\left(\tan \left(\frac{3 \pi}{4}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The value of 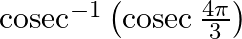 is
is
A. 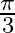
B. 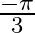
C. 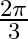
D. none of these
Solution: Option(B) is correct. To Find: The value of $\operatorname{cosec}^{-1}\left(\operatorname{cosec}\left(\frac{4 \pi}{3}\right)\right)$ Now, let...
Mark the tick against the correct answer in the following: The value of 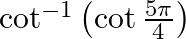 is
is
A. 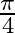
B. 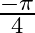
C. 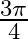
D. none of these
Solution: Option(A) is correct. To Find: The value of $\cot ^{-1}\left(\cot \left(\frac{5 \pi}{4}\right)\right)$ Now, let $x=\cot ^{-1}\left(\cot \left(\frac{5 \pi}{4}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The value of 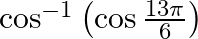 is A.
is A. 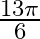 B.
B. 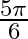 C.
C. 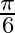 D.
D. 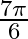
Solution: Option(C) ids correct. To Find: The value of $\cos ^{-1}\left(\cos \left(\frac{13 \pi}{6}\right)\right)$ Now, let $x=\cos ^{-1}\left(\cos \left(\frac{13 \pi}{6}\right)\right)$ $\Rightarrow...
Mark the tick against the correct answer in the following: The principal value of 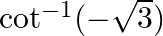 is
is
A. 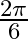
B. 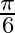
C. 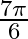
D. 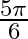
Solution: Option(D) is correct. To Find: The Principle value of $\cot ^{-1}(-\sqrt{3})$ Let the principle value be given by $\mathrm{x}$ Now, let $x=\cot ^{-1}(-\sqrt{3})$ $\begin{array}{l}...
Mark the tick against the correct answer in the following: The principal value of 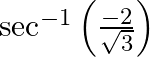 is
is
A. 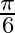
B. 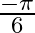
C. 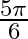
D. 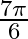
Solution: Option(C) is correct. To Find: The Principle value of $\sec ^{-1}\left(\frac{-2}{\sqrt{3}}\right)$ Let the principle value be given by $x$ Now, let $x=\sec...
Mark the tick against the correct answer in the following: The principal value of 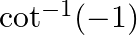 is
is
A. 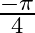
B. 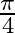
C. 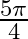
D. 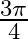
Solution: Option(D) is correct. To Find: The Principle value of $\cot ^{-1}(-1)$ Let the principle value be given by $x$ Now, let $x=\cot ^{-1}(-1)$ $\Rightarrow \cot x=-1$ $\Rightarrow \cot x=-\cot...
Mark the tick against the correct answer in the following: The principal value of 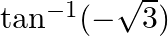 is
is
A. 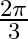
B. 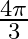
C. 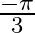
D. none of these
Solution: Option(C) is correct. To Find: The Principle value of $\tan ^{-1}(-\sqrt{3})$ Let the principle value be given by $x$ Now, let $x=\tan ^{-1}(-\sqrt{3})$ $\begin{array}{l} \Rightarrow \tan...
Draw two concentric circles of radii 4 cm and 6 cm. Construct a tangent to the smaller circle from a point on the larger circle. Measure the length of this tangent.
Draw a circle of radius 4 cm. Draw tangent to the circle making an angle of 60 with a line passing through the centre.
Draw a circle of radius 3.5 cm. Draw a pair of tangents to this circle which are inclined to each other at an angle of 60 . Write the steps of construction.
Draw a circle of radius 4.8 cm. Take a point P on it. Without using the centre of the circle, construct a tangent at the point P. Write the steps of construction.
Draw a ABC , right-angled at B such that AB = 3 cm and BC = 4cm. Now, Construct a triangle
Construct an isosceles triangle whose base is 9 cm and altitude 5cm. Construct another
Construct a ABC in which BC = 5cm, C 60 and altitude from A equal to 3 cm. Construct
Construct a ABC Sol: in which B= 6.5 cm, AB = 4.5 cm and ABC 60
Draw a line segment AB of length 6.5 cm and divided it in the ratio 4 : 7. Measure each of the two parts.
Draw a line segment AB of length 5.4 cm. Divide it into six equal parts. Write the steps of construction.
Construct a tangent to a circle of radius 4 cm form a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Draw a circle of radius 32 cm. Draw a tangent to the circle making an angle 30 with a line passing through the centre.
Write the steps of construction for drawing a pair of tangents to a circle of radius 3 cm , which are inclined to each other at an angle of 60 .
Draw a circle of radius 4.2. Draw a pair of tangents to this circle inclined to each other at an angle of 45
Draw a line segment AB of length 8 cm. Taking A as centre , draw a circle of radius 4 cm and taking B as centre , draw another circle of radius 3 cm. Construct tangents to each circle form the centre of the other circle.
Draw a circle with the help of a bangle. Take any point P outside the circle. Construct the pair of tangents form the point P to the circle
Draw a circle with center O and radius 4 cm. Draw any diameter AB of this circle. Construct tangents to the circle at each of the two end points of the diameter AB.
Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.
2. Draw two tangents to a circle of radius 3.5 cm form a point P at a distance of 6.2 cm form its centre.
Draw a circle of radius 3 cm. Form a point P, 7 cm away from the centre of the circle, draw two tangents to the circle. Also, measure the lengths of the tangents.
Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3
Construct an isosceles triangles whose base is 8 cm and altitude 4 cm and then another
To construct a triangle similar to
Find the (v) length of the latus rectum of each of the following ellipses. ![Rendered by QuickLaTeX.com \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c1bda8518d8de0566fb7bb8dae83e7d6_l3.png)
Given: \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\] Divide by \[16\] to both the sides, we get...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-c1bda8518d8de0566fb7bb8dae83e7d6_l3.png)
Given: \[\mathbf{16}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{16}\] Divide by \[16\] to both the sides, we get...
Find the (iii) coordinates of the foci, (iv) eccentricity ![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cd71d027e4ee356834184fd92e4f618_l3.png)
![Rendered by QuickLaTeX.com \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-2cd71d027e4ee356834184fd92e4f618_l3.png)
Given: \[\frac{{{x}^{2}}}{4}+\frac{{{y}^{2}}}{25}=1\]…(i) Since, \[4\text{ }<\text{ }25\] So, above equation is of the form, \[\frac{{{x}^{2}}}{{{b}^{2}}}+\frac{{{y}^{2}}}{{{a}^{2}}}=1\]…(ii)...
Mark the tick against the correct answer in the following: The principal value of 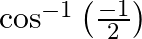 is
is
A. 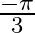
B. 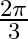
C. 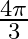
D. 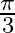
Solution: Option(B) is correct. To Find: The Principle value of $\cos ^{-1}\left(\frac{-1}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\cos ^{-1}\left(\frac{-1}{2}\right)$...
Mark the tick against the correct answer in the following: The principal value of 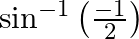 is
is
A. 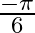
B. 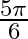
C. 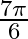
D. none of these
Solution: Option(A) is correct. To Find: The Principle value of $\sin ^{-1}\left(\frac{-1}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\sin ^{-1}\left(\frac{-1}{2}\right)$...
Mark the tick against the correct answer in the following: The principal value of 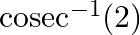 is
is
A. 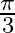
B. 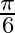
C. 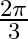
D. 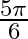
Solution: Option(B) is correct. To Find: The Principle value of $\operatorname{cosec}^{-1}(2)$ Let the principle value be given by $x$ Now, let $x=\operatorname{cosec}^{-1}(2)$ $\begin{array}{l}...
Find the (i) lengths of major axes, (ii) coordinates of the vertices ![Rendered by QuickLaTeX.com \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\]](https://www.learnatnoon.com/s/wp-content/ql-cache/quicklatex.com-862342dfce29b8b9c9392c90bd44304d_l3.png)
Given: \[\mathbf{9}{{\mathbf{x}}^{\mathbf{2}}}+\text{ }\mathbf{16}{{\mathbf{y}}^{\mathbf{2}}}=\text{ }\mathbf{144}\] Divide by \[144\] to both the sides, we get...
Mark the tick against the correct answer in the following: The principal value of 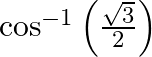 is
is
A. 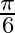
B. 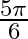
C. 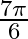
D. none of these
Solution: Option (A) is correct. To Find:The Principle value of $\cos ^{-1}\left(\frac{\sqrt{3}}{2}\right)$ Let the principle value be given by $x$ Now, let $x=\cos...
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 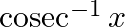
Solution: Principal value branch of $\operatorname{cosec}^{-1} x$ is $\left[-\frac{\pi}{2}, 0\right) \cup\left(0, \frac{\pi}{2}\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 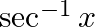
Solution: Principal value branch of $\sec ^{-1} x$ is $\left[0, \frac{\pi}{2}\right) \cup\left(\frac{\pi}{2}, \pi\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 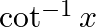
Solution: Principal value branch of $\cot ^{-1} x$ is $(0, \pi)$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 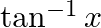
Solution: Principal value branch of $\tan ^{-1} \times$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 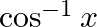
Solution: Principal value branch of $\cos ^{-1} x$ is $[0, \pi]$
Write down the interval for the principal-value branch of each of the following functions and draw its graph: 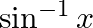
Solution: Principal value branch of $\sin ^{-1} x$ is $\left[-\frac{\pi}{2}, \frac{\pi}{2}\right]$
7. Construct a ABC in which BC = 8 cm, B 45 and C 60 . Construct another
6. Construct a ABC in which AB = 6 cm, A 30and AB 60 . Construct
Sol: Steps of Construction with base AB’ = 8 cm. Step 1: Draw a line segment AB = 6cm. Step 2: At A, draw ÐXAB = 30°. Step 3: At B, draw ÐYBA = 60°. Suppose AX and BY intersect at C. Thus, DABC is...
5. Construct a ABC with BC = 7 cm, B 60 and AB = 6 cm. Construct another triangle
Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides
3. Construct a PQR , in which PQ = 6 cm, QR = 7 cm and PR =- 8 cm. Then, construct
Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.
Draw a line segment AB of length 7 cm. Using ruler and compasses, find a point P on AB
Solve for  :
: 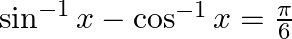
Solution: Given: $\sin ^{-1} x-\cos ^{-1} x=\frac{\pi}{6}$ We know that $\sin ^{-1} \mathrm{x}+\cos ^{-1} \mathrm{x}=\frac{\pi}{2}$ So, $\sin ^{-1} x=\frac{\pi}{2}-\cos ^{-1} x$ Substituting in the...
Solve for  :
: 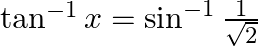
Solution: To find: value of $x$ Given: $\tan ^{-1} \mathrm{x}=\sin ^{-1} \frac{1}{\sqrt{2}}$ We know that $\sin \frac{\pi}{4}=\frac{1}{\sqrt{2}}$ Therefore, $\frac{\pi}{4}=\sin ^{-1}...
Solve for  :
: 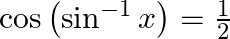
Solution: To find: value of $x$ Given: $\cos \left(\sin ^{-1} \mathrm{x}\right)=\frac{1}{2}$ $\text { LHS }=\cos \left(\sin ^{-1} x\right)$ $\begin{array}{l} =\cos \left(\cos...
Solve for  :
: 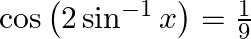
Solution: To find: value of $x$ Formula Used: $2 \sin ^{-1} x=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)$. Given: $\cos \left(2 \sin ^{-1} x\right)=\frac{1}{9}$ $\text { LHS }=\cos \left(2 \sin ^{-1}...
Solve for 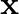 :
: 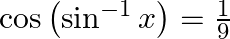
Solution: To find: value of $x$ Given: $\cos \left(\sin ^{-1} x\right)=\frac{1}{9}$ $\mathrm{LHS}=\cos \left(\sin ^{-1} \mathrm{x}\right) \ldots(1)$ Let $\sin \theta=x$ Therefore $\theta=\sin ^{-1}...
Solve for x: 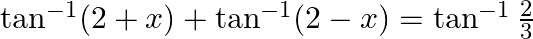
Solution: To find: value of $x$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where xy $<1$ Given: $\tan ^{-1}(2+x)+\tan ^{-1}(2-x)=\tan ^{-1} \frac{2}{3}$...
Solve for  :
: 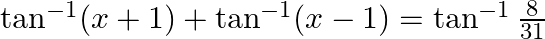
Solution: To find: value of $x$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan ^{-1}\left(\frac{\mathrm{x}+y}{1-\mathrm{xy}}\right)$ where $\mathrm{xy}<1$ Given: $\tan...
Prove that: 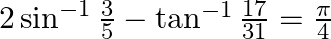
Solution: To Prove: $2 \sin ^{-1} \frac{3}{5}-\tan ^{-1} \frac{17}{31}=\frac{\pi}{4}$ Formula Used: 1) $2 \sin ^{-1} x=\sin ^{-1}\left(2 x \times \sqrt{1-x^{2}}\right)$ 2) $\tan ^{-1}...
Prove that: 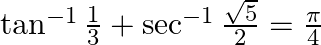
Solution: To Prove: $\tan ^{-1} \frac{1}{3}+\sec ^{-1} \frac{\sqrt{5}}{2}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x y<1$ Proof:...
Prove that: 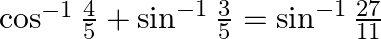
Solution: To Prove: $\cos ^{-1} \frac{4}{5}+\sin ^{-1} \frac{3}{5}=\sin ^{-1} \frac{27}{11}$ Formula Used: $\sin ^{-1} x+\sin ^{-1} y=\sin ^{-1}\left(x \times \sqrt{1-y^{2}}+y \times...
Prove that: 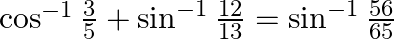
Solution: To Prove: $\cos ^{-1} \frac{3}{5}+\sin ^{-1} \frac{12}{13}=\sin ^{-1} \frac{56}{65}$ Formula Used: $\sin ^{-1} \mathrm{x}+\sin ^{-1} \mathrm{y}=\sin ^{-1}\left(\mathrm{x} \times...
Prove that: 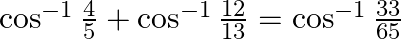
Solution: To Prove: $\cos ^{-1} \frac{4}{5}+\cos ^{-1} \frac{12}{13}=\cos ^{-1} \frac{33}{65}$ Formula Used: $\cos ^{-1} x+\cos ^{-1} y=\cos ^{-1}\left(x y-\sqrt{1-x^{2}} \times...
Prove that: 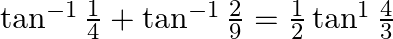
Solution: To Prove: $\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}=\frac{1}{2} \tan ^{-1} \frac{4}{3} \Rightarrow 2\left(\tan ^{-1} \frac{1}{4}+\tan ^{-1} \frac{2}{9}\right)=\tan ^{-1} \frac{4}{3}$...
Prove that: 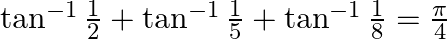
Solution: To Prove: $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{5}+\tan ^{-1} \frac{1}{8}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ where $x...
Prove that: 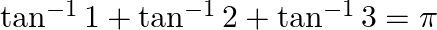
Solution: To Prove: $\tan ^{-1} 1+\tan ^{-1} 2+\tan ^{-1} 3=\pi$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\pi+\tan ^{-1}\left(\frac{\mathrm{x}+\mathrm{y}}{1-\mathrm{xy}}\right)$...
Prove that: 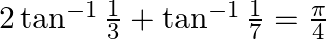
Solution: To Prove: $2 \tan ^{-1} \frac{1}{3}+\tan ^{-1} \frac{1}{7}=\frac{\pi}{4}$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan...
Prove that: 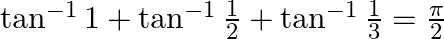
Solution: To Prove: $\tan ^{-1} 1+\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}=\frac{\pi}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ Proof:...
Prove that: 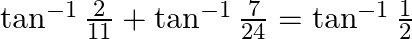
Solution: To Prove: $\tan ^{-1} \frac{2}{11}+\tan ^{-1} \frac{7}{24}=\tan ^{-1} \frac{1}{2}$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan ^{-1}\left(\frac{x+y}{1-x y}\right)$ Proof:...
Prove that: 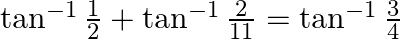
Solution: To Prove: $\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{2}{11}=\tan ^{-1} \frac{3}{4}$ Formula Used: $\tan ^{-1} \mathrm{x}+\tan ^{-1} \mathrm{y}=\tan...
Prove that: 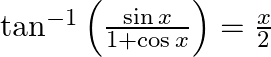
Solution: To Prove: $\tan ^{-1}\left(\frac{\sin x}{1+\cos x}\right)=\frac{x}{2}$ Formula Used: 1) $\sin A=2 \times \sin \frac{A}{2} \times \cos \frac{A}{2}$ 2) $1+\cos A=2 \cos ^{2} \frac{A}{2}$...
Prove that: 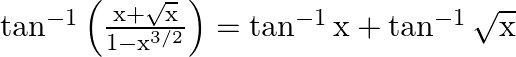
Solution: We know that, $\tan ^{-1}\left(\frac{A+B}{1-A B}\right)=\tan ^{-1} A+\tan ^{-1} B$ Now, taking $A=x$ and $B=\sqrt{x}$ We get, $\tan ^{-1} x+\tan ^{-1} \sqrt{x}=\tan...
Prove that: 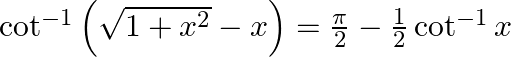
Solution: To Prove: $\cot ^{-1}\left(\sqrt{1+x^{2}}-x\right)=\frac{\pi}{2}-\frac{1}{2} \cot ^{-1} x$ Formula Used: 1) $\tan \left(\frac{\pi}{4}+A\right)=\frac{1+\tan A}{1-\tan A}$ 2)...
Prove that: 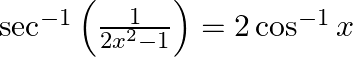
Solution: To Prove: $\sec ^{-1}\left(\frac{1}{2 x^{2}-1}\right)=2 \cos ^{-1} x$ Formula Used: 1) $\cos 2 A=2 \cos ^{2} A-1$ 2) $\cos ^{-1} A=\sec ^{-1}\left(\frac{1}{A}\right)$ Proof:...
Prove that: 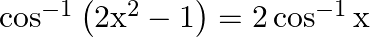
Solution: To Prove: $\cos ^{-1}\left(2 x^{2}-1\right)=2 \cos ^{-1} x$ Formula Used: $\cos 2 A=2 \cos ^{2} A-1$ Proof: $\text { LHS }=\cos ^{-1}\left(2 x^{2}-1\right) \ldots(1)$ Let $x=\cos A \ldots$...
Prove that: 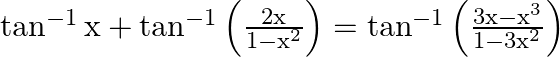
Solution: To Prove: $\tan ^{-1} x+\tan ^{-1}\left(\frac{2 x}{1-x^{2}}\right)=\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)$ Formula Used: $\tan ^{-1} x+\tan ^{-1} y=\tan...
Prove that: 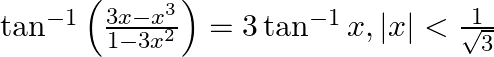
Solution: To Prove: $\tan ^{-1}\left(\frac{3 x-x^{3}}{1-3 x^{2}}\right)=3 \tan ^{-1} x$ Formula Used: $\tan 3 A=\frac{3 \tan A-\tan ^{3} A}{1-3 \tan ^{2} A}$ Proof: $\text { LHS }=\tan...
Prove that: 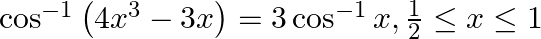
Solution: To Prove: $\cos ^{-1}\left(4 x^{3}-3 x\right)=3 \cos ^{-1} x$ Formula Used: $\cos 3 A=4 \cos ^{3} A-3 \cos A$ Proof: $\text { LHS }=\cos ^{-1}\left(4 x^{3}-3 x\right) \ldots(1)$ Let...
Prove that: 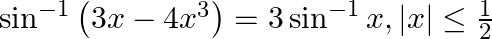
Solution: To Prove: $\sin ^{-1}\left(3 x-4 x^{3}\right)=3 \sin ^{-1} x$ Formula Used: $\sin 3 \mathrm{~A}=3 \sin \mathrm{A}-4 \sin ^{3} \mathrm{~A}$ Proof: $\operatorname{LHS}=\sin ^{-1}\left(3 x-4...
Prove that: 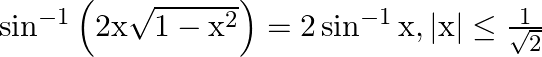
Solution: To Prove: $\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)=2 \sin ^{-1} x$ Formula Used: $\sin 2 A=2 \times \sin A \times \cos A$ Proof: $\text { LHS }=\sin ^{-1}\left(2 x \sqrt{1-x^{2}}\right)...
Prove that: 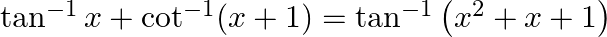
Solution: To Prove: $\tan ^{-1} x+\cot ^{-1}(x+1)=\tan ^{-1}\left(x^{2}+x+1\right)$ Formula Used: 1) $\cot ^{-1} \mathrm{x}=\tan ^{-1} \frac{1}{\mathrm{x}}$ 2) $\tan ^{-1} \mathrm{x}+\tan ^{-1}...
Find the principal value of each of the following: 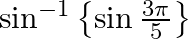
Solution: $\begin{array}{l} \sin ^{-1}\left\{\sin \left(\frac{3 \pi}{5}\right)\right\} \\ =\sin ^{-1}\left\{\sin \left(\pi-\frac{2 \pi}{5}\right)\right\} \end{array}$ [Formula: $\sin (\pi-x)=\sin...
Find the principal value of each of the following : 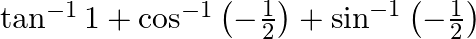
Solution: [Formula: $\cos ^{-1}(-x)=\pi-\cos (x)$ and $\left.\sin ^{-1}(-x)=-\sin (x)\right]$ $\tan ^{-1} 1+\left(\pi-\cos ^{-1}\left(\frac{1}{2}\right)\right)+\left(-\sin...
Find the principal value of each of the following : 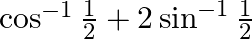
Solution: Putting the values of the inverse trigonometric terms $\begin{array}{l} \frac{\pi}{3}+2 \times \frac{\pi}{6} \\ =\frac{\pi}{3}+\frac{\pi}{3} \\ =\frac{2 \pi}{3} \end{array}$
Find the principal value of each of the following : 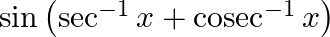
Solution: $\sin \left(\sec ^{-1} x+\operatorname{cosec}^{-1} x\right)=\sin \left(\frac{\pi}{2}\right)$ [Formula: $\left.\sec ^{-1} x+\operatorname{cosec}^{-1} x=\frac{\pi}{2}\right]$ Putting the...
Find the principal value of each of the following : 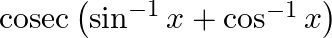
Solution: $\operatorname{cosec}\left(\sin ^{-1} x+\cos ^{-1} x\right)=\operatorname{cosec} \frac{\pi}{2}\left[\right.$ Formula: $\left.\sin ^{-1} x+\cos ^{-1} x=\frac{\pi}{2}\right]$ Putting the...
Find the principal value of each of the following: 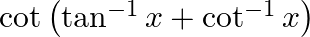
Solution: $\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)=\cot \left(\frac{\pi}{2}\right)$ [Formula: $\left.\tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}\right]$ Putting value of $\cot...
Find the principal value of each of the following : 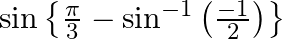
Solution: $\begin{array}{l} \sin \left\{\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right\}\left[\text { Formula: } \sin ^{-1}(-\mathrm{x})=-\sin ^{-1} \mathrm{x}\right] \\ =\sin...
Find the principal value of each of the following : 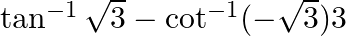
Solution: $\tan ^{-1} \sqrt{3}-\cot ^{-1}(-\sqrt{3})$ Putting the value of $\tan ^{-1} \sqrt{3}$ and using the formula $\begin{array}{l} \cot ^{-1}(-x)=\pi-\cot ^{-1} x \\...
Find the principal value of each of the following : 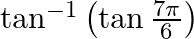
Solution: $\tan ^{-1}\left(\tan \frac{7 \pi}{6}\right)=\tan ^{-1}\left(\tan \left(\pi+\frac{\pi}{6}\right)\right)$ [ Formula: $\tan (\pi+x)=\tan x$, as tan is positive in the third quadrant.] $=\tan...
Find the principal value of each of the following : 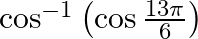
Solution: $\cos ^{-1}\left(\cos \frac{13 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2 \pi+\frac{\pi}{6}\right)\right)$ [ Formula: $\cos (2 \pi+x)=\cos x, \cos$ is positive in the first quadrant. ]...
Find the principal value of each of the following : 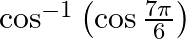
Solution: $\cos ^{-1}\left(\cos \frac{7 \pi}{6}\right)=\cos ^{-1}\left(\cos \left(2 \pi-\frac{5 \pi}{6}\right)\right)$ [Formula: $\cos (2 \pi-x)=\cos (x)$, as cos has a positive vaule in the fourth...
Find the principal value of each of the following : 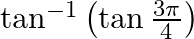
Solution: $\tan ^{-1}\left(\tan \frac{3 \pi}{4}\right)=\tan ^{-1}\left(\tan \left(\pi-\frac{\pi}{4}\right)\right)$ [Formula: $\tan (\pi-x)=-\tan (x)$, as tan is negative in the second quadrant. ]...
Find the principal value of each of the following : 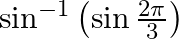
Solution: $\sin ^{-1}\left(\sin \frac{2 \pi}{3}\right)=\sin ^{-1}\left(\sin \left(\pi-\frac{\pi}{3}\right)\right)$ [ Formula: $\sin (\pi-x)=\sin x)$ $=\sin ^{-1}\left(\sin \frac{\pi}{3}\right)$ [...
Find the principal value of each of the following : 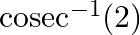
Solution: $\operatorname{cosec}^{-1}(2)$ Putting the value directly $=\frac{\pi}{6}$
Find the principal value of each of the following : 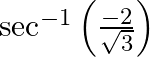
Solution: $\sec ^{-1}\left(\frac{-2}{\sqrt{3}}\right)=\pi-\sec ^{-1}\left(\frac{2}{\sqrt{3}}\right)\left[\right.$ Formula: $\left.\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)\right]$ $\begin{array}{l}...
Find the principal value of each of the following : 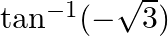
Solution: $\tan ^{-1}(-\sqrt{3})=-\tan ^{-1}(\sqrt{3})$ [Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ $=-\frac{\pi}{3}$
Find the principal value of each of the following : 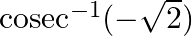
Solution: $\operatorname{cosec}^{-1}(-\sqrt{2})=-\operatorname{cosec}^{-1}(\sqrt{2})$ [Formula: $\left.\operatorname{cosec}^{-1}(-x)=-\operatorname{cosec}^{-1}(x)\right]$ $=-\frac{\pi}{4}$ This can...
Find the principal value of each of the following : 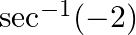
Solution: $\sec ^{-1}(-2)=\pi-\sec ^{-1}(2)\left[\right.$ Formula: $\left.\sec ^{-1}(-x)=\pi-\sec ^{-1}(x)\right]$ $\begin{array}{l} =\pi-\frac{\pi}{3} \\ =\frac{2 \pi}{3} \end{array}$
Find the principal value of each of the following : 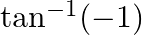
Solution: $\tan (-1)=-\tan (1)\left[\right.$ Formula: $\left.\tan ^{-1}(-x)=-\tan ^{-1}(x)\right]$ [ We know that $\tan \frac{\pi}{4}=1$, thus $\left.\tan ^{-1} \frac{\pi}{4}=1\right]$...
Find the principal value of each of the following : 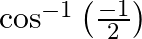
Solution: $\cos ^{-1}\left(\frac{-1}{2}\right)=\pi-\cos ^{-1}\left(\frac{1}{2}\right)$ [ Formula: $\left.\cos ^{-1}(-x)=-\cos ^{-1}(x)\right]$ $=\pi-\frac{\pi}{3}$ $=\frac{2 \pi}{3}$
Find the principal value of each of the following : 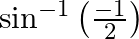
Solution: $\sin ^{-1}\left(\frac{-1}{2}\right)=-\sin ^{-1}\left(\frac{1}{2}\right)\left[\right.$ Formula: $\left.\sin ^{-1}(-x)=\sin ^{-1}(x)\right]$ $=-\frac{\pi}{6}$
Find the modulus of each of the following complex numbers and hence express each of them in polar form:
If z2 + |z|2 = 0, show that z is purely imaginary.
Find the probability that a leap year selected at random w ill contain 53 Sundays.
A game consists o f tossing a 1 rupee coin three times, and noting Its outcomes each time. Find the probability o f getting (I) 3 heads, (II) at least 2 tails.
All kings, queens, and aces are removed from a pack o f 52 cards. The remaining cards are well-shuffled and then a card Is drawn from I t Find the probability that the drawn card Is
(I) a black face card,
(II)a red face card.
All red face cards are removed from a pack o f playing cards. The remaining cards are well-shuffled and then a card Is drawn at random from them. Find the probability that the drawn card Is
(I) a red card,
(II) a face card,
(III)a card of clubs.
What Is the probability that an ordinary year has 53 Mondays?
A card Is drawn at random from a well-shuffled pack o f 52 cards. Find the probability that the card was drawn Is neither a red card nor a queen.
5 cards the ten, Jack, queen, king and ace o f diamonds are well shuffled with their faces downward. One card Is then picked up at random. (a) What Is the probability that the drawn card Is the queen? (b) If the queen Is drawn and put aside and a second card Is drawn, find the probability that the second card Is (I) an ace, (II) a queen.
A letter Is chosen at random from the letter o f the word ‘ASSOCIATION’. Find the probability that the chosen letter Is a (I) vowel (II) consonant (III) S
Two dice are rolled once. Find the probability o f getting such numbers on 2 dice whose product Is a perfect square.
A die Is rolled twice. Find the probability that _9_ _ 3 12 4
(I) 5 w ill not come up either time,
(II) 5 w ill come up exactly one time,
(III) 5 w ill come up both the times.
A group consists o f 12 persons, o f which 3 are extremely patient, other 6 are extremely honest and rest are extremely kind. A person from the group Is selected at random. Assuming that each person Is equally likely to be selected, find the probability o f selecting a person who Is
(I) extremely patient,
(II) extremely kind o r honest. Which o f the above values did you prefer more?
A carton consists o f 100 shirts o f which 88 are good and 8 have minor defects. Rohlt, a trader, w ill only accept the shirts which are good. But, Kamal, and another trader w ill only reject the shirts which have major defects. 1 shirt Is drawn at random from the carton. What Is the probability that It Is acceptable to
(I)Rohlt,
(II) Kamal?
A Jar contains 54 marbles, each o f which some are blue, some are green and some are white. The probability o f selecting a blue marble at random Is and the probability o f selecting a green marble at random Is | . How many white marbles does the Jar contain?
A Jar contains 24 marbles. Some o f these are green others are blue. If a marble Is drawn at random from the Jar, the probability that It Is green Is | . Find the number o f blue marbles In the Jar.
A bag contains 18 balls out o f which x balls are red.
(I)If one ball Is drawn at random from the bag, what Is the probability that It Is not red?
(II) If two more red balls are put In the bag, the probability o f drawing a red ball w ill be | times the probability o f drawing a red ball In the firs t case. Find the value o f x.
Find the equation of the circle of radius 5 cm, whose centre lies on the y – axis and which passes through the point (3, 2).
Answer: The general form of the equation of a circle is (x - h)2 + (y - k)2 = r2 (h, k) is the centre of the circle. r is the radius of the circle. The centre lies on Y - axis, ∴ it’s X - coordinate...
The probability o f selecting a red ball at random from a Jar that contains only red, blue and orange balls Is j . The probability of selecting a blue ball at random from the same Jar Is j .If the Jar contains 10 orange balls, find the total number o f balls In the Jar.
A piggy bank contains hundred 50-p coins, seventy Rs. 1 coin, fifty Rs. 2 coins and th irty Rs. 5 coins. If It Is equally likely that one of the coins will fall out when the blank Is turned upside down, what Is the probability that the coin(I) will bea R s. 1 coin? (II) will not be a Rs. 5 coin (III) will be 50-p or a Rs. 2 coin?
A box contains 80 discs, which are numbered from 1 to 80. If one disc Is drawn at random from the box, find the probability that It bears a perfect square number.
Tickets numbered 2 ,3 ,4 , 5……………100,101 are placed In a box and mix thoroughly. One ticket Is drawn at random from the box. Find the probability that the number on the ticket Is(III) a number which Is a perfect square (Iv) a prime number less than 40.
Tickets numbered 2 ,3 ,4 , 5……………100,101 are placed In a box and mix thoroughly. One ticket Is drawn at random from the box. Find the probability that the number on the ticket Is
(I)an even number
(II)a number less than 16
Cards marked with numbers 1,3, 5……………..101 are placed In a bag and mixed thoroughly. A card Is drawn at random from the bag. Find the probability that the number on the drawn card Is
(I)less than 19,
(II) a prime number less than 20.
A box contains cards bearing numbers 6 to 70. If one card Is drawn at random from the box, find the probability that It bearsA box contains cards bearing numbers 6 to 70. If one card Is drawn at random from the box, find the probability that It bearsA box contains cards bearing numbers 6 to 70. If one card Is drawn at random from the box, find the probability that It bears
(III) an odd number less than 30,
(Iv) a composite number between 50 and 70.
A box contains cards bearing numbers 6 to 70. If one card Is drawn at random from the box, find the probability that It bears
(I) a 1 digit number,
(II)a number divisible by 5,
Cards bearing numbers 1,3, 5……………..35 are kept In a bag. A card Is drawn at random from the bag. Find the probability o f getting a card bearing
(I)a prime number less than 15,
(II) a number divisible by 3 and 5.
Card numbered 1 to 30 are put In a bag. A card Is drawn at random from the bag. Find the probability that the number on the drawn card Is
(I) not divisible by 3,
(II)a prime number greater than 7,
(III)not a perfect square number.
A box contains cards numbered 3, 5 , 7 , 9 ……..35,37. A card Is drawn at random from the box. Find the probability that the number on the card Is a prime number.
A box contains 25 cards numbers from 1 to 25. A card Is drawn at random from the bag. Find the probability that the number on the drawn card Is(I) divisible by 2 or 3, (II) a prime number.
A card Is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card was drawn Is
(III)either a king or queen
(Iv) neither a king nor the queen.
A card Is drawn at random from a well-shuffled deck o f playing cards. Find the probability that the card was drawn Is
(I)a card of a spade or an Ace
(II)a red king
One card Is drawn from a well-shuffled deck of 52 cards. Find the probability o f getting(v) a Jack o f hearts (vl) a spade.
One card Is drawn from a well-shuffled deck of 52 cards. Find the probability o f getting
(III)a red face card
(Iv) a queen o f black suit
One card Is drawn from a well-shuffled deck of 52 cards. Find the probability o f getting
(I)a king o f red suit
(II) a face card
There are 40 students In a class o f whom 25 are girls and 15 are boys. The class teacher has to select one student as a class representative. He writes the name o f each student on a separate, the card being Identical. Then she puts cards In a bag and stirs them thoroughly. She then draws one card from the bag. What Is the probability that the name written on the card Is the name of
(I) A girl?
(II)A boy?
A bag contains lemon-flavored candles only. Hema takes out 1 candy without looking Into the bag. What Is the probability that she takes out
(I)An orange-flavored candy
(II)A lemon-flavored candy
(I) A lo t o f 20 bulbs contain 4 defective ones. 1 bulb Is drawn at random from the lot. What Is the probability that this bulb Is defective? (II) Suppose the ball drawn In
(I) Is not defective and not replaced. Now, ball Is drawn at random from the rest. What Is the probability that this bulb Is not defective?
A box contains 90 discs which are numbered from 1 to 90 If one disc Is drawn at random from the box, find the probability that It bears
(I) A two-digit number
(II) A perfect square number
(III) A number divisible by 5.
A lot consists o f 144 ballpoint pens o f which 20 are defective and others good. Tanvl will buy a pen If It Is a good but will not buy If It Is defective. The shopkeeper draws 1 pen at random and gives It to her. What Is the probability that
(I) She will buy It,
(II) She will not buy It?
12 defective pens are accidentally mixed with 132 good ones, It Is not possible to Just look at pen and tell whether or not It Is defective. 1 pen Is taken out at random from this lot. Find the probability that the pen taken out Is good one.
A game of chance consists of spinning and arrow which Is equally likely to come to the rest pointing to one of the numbers 1 , 2 ,3 ,4 12 as shown In the figure. What Is the probability that It will point to
(III)A prime number
(Iv) A number which Is a multiple o f 5
A game of chance consists of spinning and arrow which Is equally likely to come to the rest pointing to one of the numbers 1 , 2 ,3 ,4 12 as shown In the figure. What Is the probability that It will point to
(I)6
(II)An even number
Cards marked with numbers 5 to 50 are placed In a box and mixed thoroughly. A card Is drawn from the box at random. Find the probability that the number on the taken out card Is
Two dice are rolled together. Find the probability o f getting such numbers on the two dice whose product Is 12.
Two dice are rolled together. Find the probability o f getting such numbers on two dice whose product Is perfect square.
Solution: When two different dice are thrown, then total number of outcomes = 36. Let E be the event of getting the product of numbers, as a perfect square. These numbers are (1,1), (1,4), (2,2),...
When two dice are tossed together, find the probability that the sum o f the numbers on their tops Is less than 7.
Solution: When two different dice are thrown, the total number of outcomes = 36. Let E be the event of getting the sum of the numbers less than 7. These numbers are (1,1), (1,2), (1,3), (1,4),...
Two different dice are rolled simultaneously. Find the probability that the sum o f the numbers on the two dice Is 10.
Solution: When two different dice are thrown, the total number of outcomes = 36. Let E1 be the event of getting the sum of the numbers on the two dice is 10. These numbers are (4 ,6), (5,5)...
If 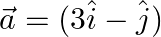 and
and 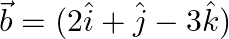 then express
then express 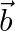 in the form
in the form  , where
, where 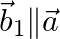 and
and  .
.
Solution: $\begin{array}{l} \vec{a}=3 \hat{\imath}-\hat{\jmath} \end{array}$ $\begin{array}{l} \mathrm{I} \vec{a} \mathrm{I}=\sqrt{3^{2}+1^{2}}=\sqrt{9+1}=\sqrt{10} \\ \hat{a}=\frac{3}{\sqrt{10}}...
If 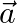 and
and 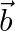 are two vectors such that
are two vectors such that 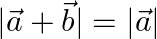 then prove that vector
then prove that vector 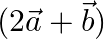 is perpendicular to the vector
is perpendicular to the vector 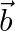 .
.
Solution: $\begin{array}{l} \mathrm{I} \vec{a}+\vec{b} \mathrm{I}=\vec{a} \\ (\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=\vec{a} \cdot \vec{a} \\ \mathrm{I} \vec{a} \mathrm{I}_{2}+\vec{a} \cdot...
If 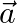 and
and 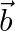 are two unit vectors such that
are two unit vectors such that 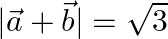 , find
, find 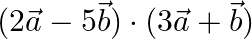 .
.
Solution: $\vec{a}$ and $\vec{b}$ are unit vectors $\begin{array}{l} (\vec{a}+\vec{b}) \cdot(\vec{a}+\vec{b})=\mathrm{I}(\vec{a}+\vec{b}) \mathrm{I}_{2} \\ \mathrm{I} \vec{a}...
Three vertices of a triangle are 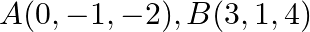 and
and 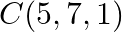 . Show that it is a right – angled triangle. Also, find its other two angles.
. Show that it is a right – angled triangle. Also, find its other two angles.
Solution: $\overrightarrow{O A}=-\hat{\jmath}-2 \hat{k}$ $\overrightarrow{O B}=3 \hat{\imath}+\hat{\jmath}+4 \hat{k}$ $\overrightarrow{O C}=5 \hat{\imath}+7 \hat{\jmath}+\hat{k}$ $\overrightarrow{O...
Find the value of 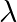 for which the vectors
for which the vectors 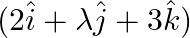 and
and 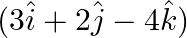 are perpendicular to each other.
are perpendicular to each other.
Solution: $\begin{array}{l} \vec{a}=2 \hat{\imath}+\lambda \hat{\jmath}+3 \hat{k} \\ \vec{b}=3 \hat{\imath}+2 \hat{\jmath}-4 \hat{k} \end{array}$ Given $\vec{a} \perp \vec{b}$ $\begin{array}{l}...
If 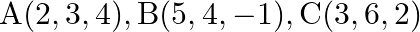 and
and 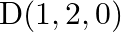 be four points, show that
be four points, show that 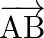 is perpendicular to
is perpendicular to  .
.
Solution: $\begin{array}{l} \overrightarrow{O A}=2 \hat{\imath}+3 \hat{\jmath}+4 \hat{k} \\ \overrightarrow{O B}=5 \hat{\imath}+4 \hat{\jmath}-\hat{k} \\ \overrightarrow{O C}=3 \hat{\imath}+6...
If 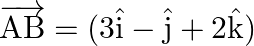 and the coordinates of
and the coordinates of 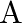 are
are 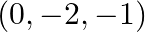 , find the coordinates of
, find the coordinates of 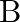 .
.
Solution: $\begin{array}{l} \overrightarrow{A B}=3 \hat{\imath}-\hat{\jmath}+2 \hat{k} \\ \overrightarrow{O A}=-2 \hat{\jmath}-\hat{k} \\ \overrightarrow{A B}=\overrightarrow{O B}-\overrightarrow{O...
The dot products of a vector with the vector 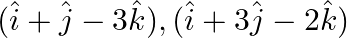 and
and 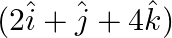 are 0,5 and 8 respectively. Find the vector.
are 0,5 and 8 respectively. Find the vector.
Solution: $\begin{array}{l} \vec{v}=\mathrm{v} 1 \hat{\imath}+\mathrm{v} 2 \hat{\jmath}+\mathrm{v}_{3} \hat{k} \\ \vec{a}=\hat{\imath}+3 \hat{\jmath}-2 \hat{k} \\...
If 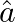 and
and 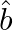 are unit vectors inclined at an angle
are unit vectors inclined at an angle 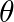 then prove that:
then prove that:
i. 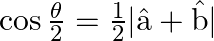
ii. 
Solution: $\hat{a}$ and $\hat{b}$ are unit vectors inclined at an angle $\theta$ i) $\begin{aligned} &(\hat{a}+\hat{b})(\hat{a}+\hat{b})=\mathrm{I} \hat{\mathrm{a}} \mathrm{I}_{2}+\mathrm{I}...
If 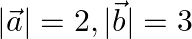 and
and 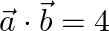 , find
, find 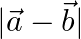 .
.
Solution: $\mathrm{I} \overrightarrow{\mathrm{a}} \mathrm{I}=2$ $\mathrm{I} \vec{b} \mathrm{I}=3$ $\vec{a} \cdot \vec{b}=4$ $(\vec{a}-\vec{b}) \cdot(\vec{a}-\vec{b})=\mathrm{I} \vec{a}...
Find the angle between 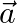 and
and 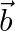 , when
, when
i.  and
and 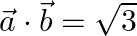
ii. 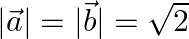 and
and 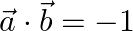
Solution: i) $\mathrm{I} \vec{a} \mathrm{I}=2$ $\mid \vec{b} \mathrm{I}=1$ $\vec{a} \cdot \vec{b}=\sqrt{3}$ $\mathrm{I} \vec{a} \mathrm{I} . \mid \vec{b} \mathrm{I} \cos \theta=\sqrt{3}$ $2 \cos...
Prove that 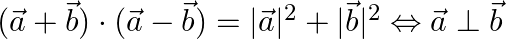 , where
, where 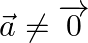 and
and 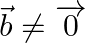 .
.
Solution: $\begin{array}{l} (\vec{a}+\vec{b}) \cdot(\vec{a}-\vec{b})=\mathrm{I} \vec{a} \mathrm{I}_{2}+\mathrm{I} \vec{b} \mathrm{I}_{2} \\ \mathrm{I} \vec{a} \mathrm{I}_{2}-\mathrm{I} \vec{b}...
Express the vector 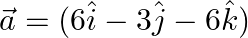 as sum of two vectors such that one is parallel to the vector
as sum of two vectors such that one is parallel to the vector 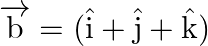 and the other is perpendicular to
and the other is perpendicular to 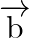 .
.
Solution: $\begin{array}{l} \vec{a}=6 \hat{\imath}-3 \hat{\jmath}-6 \hat{k} \\ \vec{b}=\hat{\imath}+\hat{\jmath}+\hat{k} \end{array}$ Let $\vec{a}$ be written as sum of $\vec{c}+\vec{d}$, where...
Find the angle between 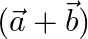 and
and 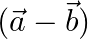 , if
, if 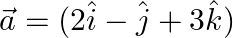 and
and 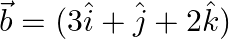 .
.
Solution: $\begin{array}{l} \text { Given: } \vec{a}=2 \hat{\imath}-\hat{\jmath}+3 \hat{k} \\ \vec{b}=3 \hat{\imath}+\hat{\jmath}+2 \hat{k} \\ \vec{a}+\vec{b}=5 \hat{\imath}+5 \hat{k} \\...
Find a vector 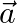 of magnitude
of magnitude 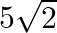 , making an angle
, making an angle 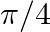 with
with  – axis,
– axis, 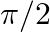 with
with  – axis and an acute angle
– axis and an acute angle 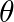 with z – axis.
with z – axis.
Solution: $\mathrm{I} \overrightarrow{\mathrm{a}} \mathrm{I}=5 \sqrt{2}$ Also it is given that $\alpha=\frac{\pi}{4}$ $\beta=\frac{\pi}{2}, \gamma=$ acute angle. So from this $\cos...
Show that the vector 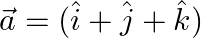 is equally inclined to the coordinate axes.
is equally inclined to the coordinate axes.
Solution: $\begin{array}{l} \vec{a}=\cos \gamma=\frac{1}{\sqrt{3}} \\ \mathrm{I} \vec{a} \mathrm{I}=\sqrt{1^{2}+1^{2}+1^{2}}=\sqrt{3} \end{array}$ Since direction cosines or cosines of angle made by...
Find the angles which the vector 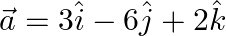 makes with the coordinate axes.
makes with the coordinate axes.
Solution: Direction cosines gives the angle made by the vector with $x$-axis, $y-$ axis, z-axis respectively. $\begin{array}{l} \vec{a}=3 \hat{\imath}-6 \hat{\jmath}+2 \hat{k} \\ \mathrm{I} \vec{a}...
If 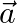 is a unit vector such that
is a unit vector such that  , find
, find 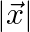 .
.
Solution: Given: $\mathrm{I} \vec{a} \mathrm{I}=1$ $\begin{array}{l} (\vec{x}-\vec{a}) \cdot(\vec{x}+\vec{a})=8 \\ \vec{x} \cdot \vec{x}+\vec{x} \cdot \vec{a}-\vec{a} \cdot \vec{x}-\vec{a} \cdot...
If 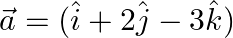 and
and 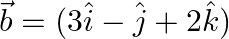 then calculate the angle between
then calculate the angle between 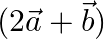 and
and 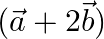 .
.
Solution: $\vec{a}=\hat{\imath}+2 \hat{\jmath}-3 \hat{k}$ $\vec{b}=3 \hat{\imath}-\hat{\jmath}+2 \hat{k}$ $\begin{array}{l}2 \vec{a}+\vec{b} & =2(\hat{\imath}+2 \hat{\jmath}-3 \hat{k})+(3...
Find the angle between the vectors 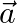 and
and 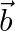 , when
, when
i. 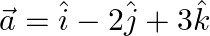 and
and 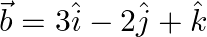
ii. 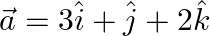 and
and 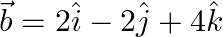
iii. 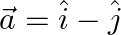 and
and 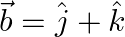 .
.
Solution: $\begin{array}{l} \text { i) } \vec{a}=\hat{\imath}-2 \hat{\jmath}+3 \hat{k} \\ \vec{b}=3 \hat{\imath}-2 \hat{\jmath}+\hat{k} \\ \mathrm{I} \vec{a}...
Write the projection of vector 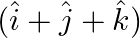 along the vector
along the vector 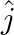 .
.
Solution: $\begin{array}{l} \vec{a}=\hat{\imath}+\hat{\jmath}+\hat{k} \\ \vec{b}=\hat{\jmath} \end{array}$ $\mathrm{I} \vec{a} \mathrm{I}=\sqrt{3}=\sqrt{1^{2}+1^{2}+1^{2}}$ $\begin{array}{l}...
Let 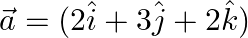 and
and 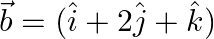 . Find the projection of (i)
. Find the projection of (i) 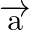 on
on 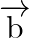 and (ii)
and (ii) 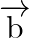 on
on 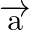 .
.
Solution: If $\vec{a}=\mathrm{a} 1 \hat{\imath}+\mathrm{a} 2 \hat{\jmath}+\mathrm{a}_{3} \hat{k}$ and $\vec{b}=\mathrm{b}_{1} \hat{\imath}+\mathrm{b}_{2} \hat{\jmath}+\mathrm{b}_{3} \hat{k}$, then...
